题目内容
12.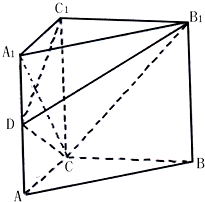 某家居装饰设计的形状是如图所示的直三棱柱ABC-A1B1C1,其中,∠ACB=90°,BCC1B1是边长为2(单位:米)的正方形,AC=1,点D为棱AA1上的动点.
某家居装饰设计的形状是如图所示的直三棱柱ABC-A1B1C1,其中,∠ACB=90°,BCC1B1是边长为2(单位:米)的正方形,AC=1,点D为棱AA1上的动点.(Ⅰ)现需要对该装饰品的表面进行涂漆处理,假设每平方米的油漆费是40元,则需油漆费多少元?(提示:$\sqrt{5}≈2.236$,结果保留到整数位)
(Ⅱ)当点D为何位置时,CD⊥平面B1C1D?
分析 (Ⅰ)证明AC⊥BC.AA1⊥BC.然后证明BC⊥平面ACC1A1.求出直三棱柱ABC-A1B1C1的表面积,即可求解需油漆费.
(Ⅱ)当点D为AA1的中点时,CD⊥平面B1C1D.当CD⊥C1D时,有CD⊥平面B1C1D,求出AD,推出结果即可.
解答 (本题满分12分)
解:(Ⅰ)因为BCC1B1是边长为2的正方形,所以BC=CC1=AA1=2.
因为∠ACB=90°,所以AC⊥BC.
又易知AA1⊥平面ABC,所以AA1⊥BC.
又AC∩AA1=A,所以BC⊥平面ACC1A1.
又AC=1,所以直三棱柱ABC-A1B1C1的表面积为${S_{ABC-{A_1}{B_1}{C_1}}}=\frac{1}{2}×2×1×2+2×2+1×2+\sqrt{{2^2}+{1^2}}×2=8+2\sqrt{5}$(平方米).
则需油漆费$({8+2\sqrt{5}})×40=320+80\sqrt{5}≈320+80×2.236≈499$(元).…(6分)
(Ⅱ)当点D为AA1的中点时,CD⊥平面B1C1D.证明如下:
由(Ⅰ)得BC⊥平面ACC1A1.
又BC∥B1C1,所以B1C1⊥平面ACC1A1.
所以B1C1⊥CD.
故当CD⊥C1D时,有CD⊥平面B1C1D,且此时有△C1A1D∽△DAC.
设AD=x,则$\frac{{{A_1}{C_1}}}{{{A_1}D}}=\frac{AD}{AC}$,即$\frac{1}{2-x}=\frac{x}{1}$,解得x=1.
此时$AD=1=\frac{1}{2}A{A_1}$,即当点D为AA1的中点时,CD⊥平面B1C1D.…(12分)
点评 本题考查直线与平面垂直判断的应用,几何体的表面积的求法,考查计算能力.

练习册系列答案
相关题目
3.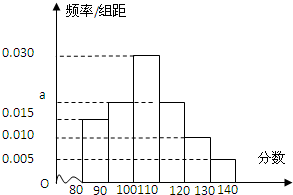 某校高一(1)班共有54人,如图是该班期中考试数学成绩的频率分布直方图,则成绩在[100,120]内的学生人数为( )
某校高一(1)班共有54人,如图是该班期中考试数学成绩的频率分布直方图,则成绩在[100,120]内的学生人数为( )
 某校高一(1)班共有54人,如图是该班期中考试数学成绩的频率分布直方图,则成绩在[100,120]内的学生人数为( )
某校高一(1)班共有54人,如图是该班期中考试数学成绩的频率分布直方图,则成绩在[100,120]内的学生人数为( )| A. | 36 | B. | 27 | C. | 22 | D. | 11 |
20.一个多面体的三视图如图所示,则该多面体的体积为( )
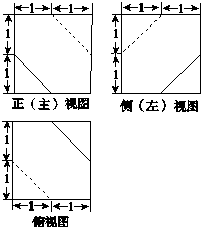

| A. | $\frac{23}{3}$ | B. | $\frac{22}{3}$ | C. | $\frac{47}{6}$ | D. | 7 |
7.若点P(x,y)的坐标x,y满足约束条件:$\left\{\begin{array}{l}x+y-6≤0\\ x-y+1≥0\\ x≥1\\ y≥1\end{array}\right.$,则$\frac{3x-4y}{5}$的最大值为( )
| A. | $-\frac{1}{5}$ | B. | -1 | C. | $\frac{11}{5}$ | D. | 11 |
17.若实数x,y满足约束条件$\left\{\begin{array}{l}y≤x\\ y≥-1\\ x+y≤1\end{array}\right.$,则z=2x-y的最大值为( )
| A. | -1 | B. | $\frac{1}{2}$ | C. | 5 | D. | 7 |
1.某商区停车场临时停车按时段收费,收费标准为:每辆汽车一次停车不超过1小时收费6元,超过1小时的部分每小时收费8元(不足1小时的部分按1小时计算).现有甲、乙二人在该商区临时停车,两人停车都不超过4小时.
(Ⅰ)设甲停车付费a元.依据题意,填写下表:
(Ⅱ)若每人停车的时长在每个时段的可能性相同,求甲、乙二人停车付费之和为36元的概率;
(Ⅲ)若甲停车1小时以上且不超过2小时的概率为$\frac{1}{3}$,停车付费多于14元的概率为$\frac{5}{12}$,求甲停车付费恰为6元的概率.
(Ⅰ)设甲停车付费a元.依据题意,填写下表:
| 甲停车时长 (小时) | (0,1] | (1,2] | (2,3] | (3,4] |
| 甲停车费a (元) |
(Ⅲ)若甲停车1小时以上且不超过2小时的概率为$\frac{1}{3}$,停车付费多于14元的概率为$\frac{5}{12}$,求甲停车付费恰为6元的概率.
18.已知函数f(x)=-x2+ax-b,若a,b都是从区间[0,3]任取的一个数,则f(1)>0成立的概率是( )
| A. | $\frac{2}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{8}{9}$ |