题目内容
8.若(x+a)10的二项展开式中含x7的项的系数为15,则实数a的值是$\frac{1}{2}$.分析 在二项展开式的通项公式中,令x的幂指数等于3,求出r的值,即可求得x7的系数,再根据x7的系数为15,求得a的值.
解答 解:(x+a)10的展开式的通项公式为 Tr+1=C10r•x10-r•ar,
令10-r=7,求得r=3,可得x7的系数为a3•C103=120a3=15,
∴a=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
18.已知函数$f(x)=sin(ωx+\frac{π}{4})(ω>0)$的最小正周期为$\frac{π}{2}$,则该函数的图象( )
| A. | 关于点($\frac{3π}{16}$,0)对称 | B. | 关于直线x=$\frac{π}{4}$ | ||
| C. | 关于点($\frac{π}{16}$,0)对称 | D. | 关于直线x=$\frac{3π}{16}$对称 |
3.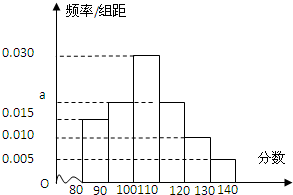 某校高一(1)班共有54人,如图是该班期中考试数学成绩的频率分布直方图,则成绩在[100,120]内的学生人数为( )
某校高一(1)班共有54人,如图是该班期中考试数学成绩的频率分布直方图,则成绩在[100,120]内的学生人数为( )
 某校高一(1)班共有54人,如图是该班期中考试数学成绩的频率分布直方图,则成绩在[100,120]内的学生人数为( )
某校高一(1)班共有54人,如图是该班期中考试数学成绩的频率分布直方图,则成绩在[100,120]内的学生人数为( )| A. | 36 | B. | 27 | C. | 22 | D. | 11 |
20.一个多面体的三视图如图所示,则该多面体的体积为( )
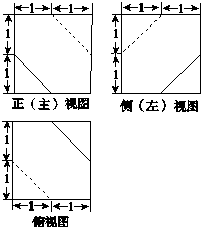

| A. | $\frac{23}{3}$ | B. | $\frac{22}{3}$ | C. | $\frac{47}{6}$ | D. | 7 |
17.若实数x,y满足约束条件$\left\{\begin{array}{l}y≤x\\ y≥-1\\ x+y≤1\end{array}\right.$,则z=2x-y的最大值为( )
| A. | -1 | B. | $\frac{1}{2}$ | C. | 5 | D. | 7 |