题目内容
已知三次函数 在y轴上的截距是2,且在
在y轴上的截距是2,且在 上单调递增,在(-1,2)上单调递减.
上单调递增,在(-1,2)上单调递减.
(Ⅰ)求函数f (x)的解析式; (Ⅱ)若函数 ,求
,求 的单调区间.
的单调区间.
 在y轴上的截距是2,且在
在y轴上的截距是2,且在 上单调递增,在(-1,2)上单调递减.
上单调递增,在(-1,2)上单调递减.
|
 ,求
,求 的单调区间.
的单调区间.(Ⅰ) 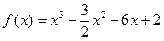 ,…………5分
,…………5分
(Ⅱ)当m≤-2时,h(x)在(-m,+∞)上单增;当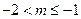 时,
时, 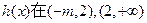 上单增;当m >-1时,在(1,2),(2,+∞)上单增;在(-m,1)单减.
上单增;当m >-1时,在(1,2),(2,+∞)上单增;在(-m,1)单减.
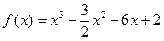 ,…………5分
,…………5分(Ⅱ)当m≤-2时,h(x)在(-m,+∞)上单增;当
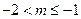 时,
时, 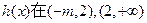 上单增;当m >-1时,在(1,2),(2,+∞)上单增;在(-m,1)单减.
上单增;当m >-1时,在(1,2),(2,+∞)上单增;在(-m,1)单减.(Ⅰ)∵ 在y轴上的截距是2,∴f(0)=2,∴c="2." 1分
在y轴上的截距是2,∴f(0)=2,∴c="2." 1分
又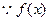 在
在 上单调递增,(-1,2)上单调递减,
上单调递增,(-1,2)上单调递减,
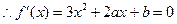 有两个根为-1,2,
有两个根为-1,2,
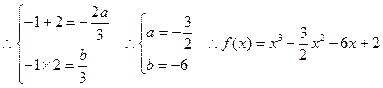 ,…………5分
,…………5分
(Ⅱ) ,
,
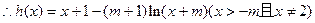 ,………………6分
,………………6分
 ,……………………………………… 7分
,……………………………………… 7分
当m≤-2时,-m≥2,定义域: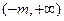 ,
,
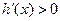 恒成立,
恒成立,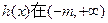 上单增; ……………………… 8分
上单增; ……………………… 8分
当 时,
时, ,定义域:
,定义域:
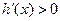 恒成立,
恒成立,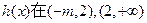 上单增……………………… 9分
上单增……………………… 9分
当m >-1时,-m <1,定义域:
由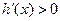 得x >1,由
得x >1,由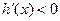 得x <1.
得x <1.
故在(1,2),(2,+∞)上单增;在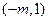 上单减. ………………11分
上单减. ………………11分
综上所述,当m≤-2时,h(x)在(-m,+∞)上单增;
当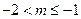 时,
时, 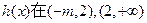 上单增;
上单增;
当m >-1时,在(1,2),(2,+∞)上单增;在(-m,1)单减.…12分
 在y轴上的截距是2,∴f(0)=2,∴c="2." 1分
在y轴上的截距是2,∴f(0)=2,∴c="2." 1分又
 在
在 上单调递增,(-1,2)上单调递减,
上单调递增,(-1,2)上单调递减,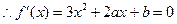 有两个根为-1,2,
有两个根为-1,2,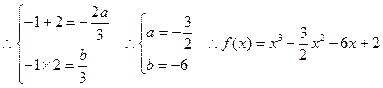 ,…………5分
,…………5分(Ⅱ)
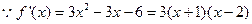 ,
,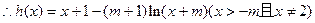 ,………………6分
,………………6分 ,……………………………………… 7分
,……………………………………… 7分当m≤-2时,-m≥2,定义域:
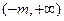 ,
,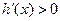 恒成立,
恒成立,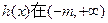 上单增; ……………………… 8分
上单增; ……………………… 8分当
 时,
时, ,定义域:
,定义域:
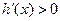 恒成立,
恒成立,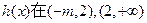 上单增……………………… 9分
上单增……………………… 9分当m >-1时,-m <1,定义域:

由
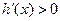 得x >1,由
得x >1,由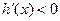 得x <1.
得x <1.故在(1,2),(2,+∞)上单增;在
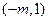 上单减. ………………11分
上单减. ………………11分综上所述,当m≤-2时,h(x)在(-m,+∞)上单增;
当
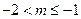 时,
时, 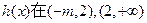 上单增;
上单增;当m >-1时,在(1,2),(2,+∞)上单增;在(-m,1)单减.…12分

练习册系列答案
相关题目
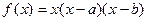 ,点A(s,f(s)), B(t,f(t))
,点A(s,f(s)), B(t,f(t))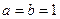 ,求函数
,求函数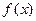 的单调递增区间;
的单调递增区间; 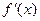 满足:当|x|≤1时,有|
满足:当|x|≤1时,有|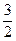 恒成立,求函数
恒成立,求函数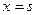 和
和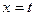 处取得极值,且
处取得极值,且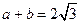 ,证明:
,证明: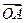 与
与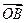 不可能垂直.
不可能垂直.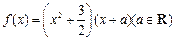 .
.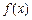 的图象上有与
的图象上有与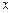 轴平行的切线,求
轴平行的切线,求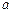 的范围;
的范围;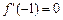 ,(Ⅰ)求函数
,(Ⅰ)求函数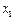 ,
,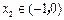 ,不等式
,不等式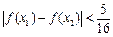 恒成立.
恒成立.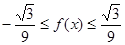 对任意的x∈[0,1]成立?若存在,求出a,b的值,若不存在,说明理由。
对任意的x∈[0,1]成立?若存在,求出a,b的值,若不存在,说明理由。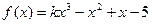 在R上单调递增,记
在R上单调递增,记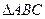 的三内角
的三内角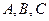 的对应边分别为
的对应边分别为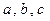 ,若
,若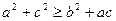 时,不等式
时,不等式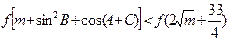 恒成立.
恒成立.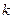 的取值范围;
的取值范围;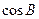 的取值范围;
的取值范围;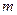 的取值范围.
的取值范围.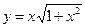 ;
;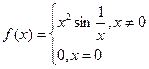 的导数
的导数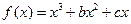 在
在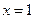 处取得极小值–2.(I)求
处取得极小值–2.(I)求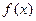 的单调区间;(II)若对任意的
的单调区间;(II)若对任意的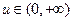 ,函数
,函数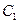 与函数
与函数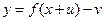 的图像
的图像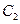 至多有一个交点.求实数
至多有一个交点.求实数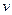 的范围.
的范围.