题目内容
已知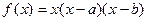 ,点A(s,f(s)), B(t,f(t))
,点A(s,f(s)), B(t,f(t))
(I) 若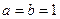 ,求函数
,求函数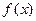 的单调递增区间;
的单调递增区间;
(II)若函数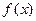 的导函数
的导函数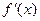 满足:当|x|≤1时,有|
满足:当|x|≤1时,有|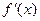 |≤
|≤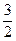 恒成立,求函数
恒成立,求函数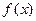 的解析表达式;
的解析表达式;
(III)若0<a<b, 函数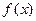 在
在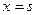 和
和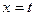 处取得极值,且
处取得极值,且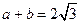 ,证明:
,证明: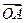 与
与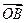 不可能垂直.
不可能垂直.
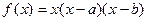 ,点A(s,f(s)), B(t,f(t))
,点A(s,f(s)), B(t,f(t))(I) 若
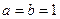 ,求函数
,求函数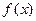 的单调递增区间;
的单调递增区间; (II)若函数
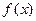 的导函数
的导函数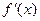 满足:当|x|≤1时,有|
满足:当|x|≤1时,有|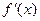 |≤
|≤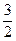 恒成立,求函数
恒成立,求函数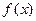 的解析表达式;
的解析表达式;(III)若0<a<b, 函数
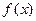 在
在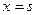 和
和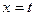 处取得极值,且
处取得极值,且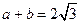 ,证明:
,证明: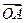 与
与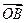 不可能垂直.
不可能垂直.(I) f(x)的增区间是(-∞,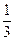 )和[1,+ ∞]. …………………………3分
)和[1,+ ∞]. …………………………3分
(II) f(x)=x3 x. ……………………9分
x. ……………………9分
(III) 证明见解析
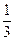 )和[1,+ ∞]. …………………………3分
)和[1,+ ∞]. …………………………3分(II) f(x)=x3
 x. ……………………9分
x. ……………………9分(III) 证明见解析
(I) f(x)=x3-2x2+x,  (x)=3x2-4x+1,
(x)=3x2-4x+1,
因为f(x)单调递增,
所以 (x)≥0,
(x)≥0,
即 3x2-4x+1≥0,
解得,x≥1, 或x≤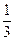 ,……………………………2分
,……………………………2分
故f(x)的增区间是(-∞,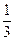 )和[1,+ ∞]. …………………………3分
)和[1,+ ∞]. …………………………3分
(II) (x)=3x2-2(a+b)x+ab.
(x)=3x2-2(a+b)x+ab.
当x∈[-1,1]时,恒有| (x)|≤
(x)|≤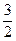 .………………………4分
.………………………4分
故有 ≤
≤ (1)≤
(1)≤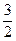 ,
,
 ≤
≤ (-1)≤
(-1)≤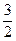 ,
,
 ≤
≤ (0)≤
(0)≤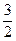 ,………………………5
,………………………5
即 ………6
………6
①+②,得
 ≤ab≤
≤ab≤ ,……………………………8分
,……………………………8分
又由③,得
ab= ,
,
将上式代回①和②,得
a+b=0,
故f(x)=x3 x. ……………………9分
x. ……………………9分
(III) 假设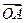 ⊥
⊥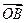 ,
,
即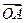
 =
= =" st+f(s)f(t)=0," ……………10分
=" st+f(s)f(t)=0," ……………10分
(s-a)(s-b)(t-a)(t-b)=-1,
[st-(s+t)a+a2][st-(s+t)b+b2]="-1," ……………………………………11分
由s,t为 (x)=0的两根可得,
(x)=0的两根可得,
s+t= (a+b), st=
(a+b), st=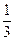 , (0<a<b),
, (0<a<b),
从而有ab(a-b)2="9." ……………………………………12分
这样(a+b)2=(a-b)2+4ab
= +4ab≥2
+4ab≥2 =12,
=12,
即 a+b≥2 ,
,
这样与a+b<2 矛盾. ……………………13分
矛盾. ……………………13分
故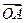 与
与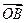 不可能垂直.
不可能垂直.
 (x)=3x2-4x+1,
(x)=3x2-4x+1,因为f(x)单调递增,
所以
 (x)≥0,
(x)≥0,即 3x2-4x+1≥0,
解得,x≥1, 或x≤
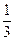 ,……………………………2分
,……………………………2分故f(x)的增区间是(-∞,
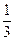 )和[1,+ ∞]. …………………………3分
)和[1,+ ∞]. …………………………3分(II)
 (x)=3x2-2(a+b)x+ab.
(x)=3x2-2(a+b)x+ab.当x∈[-1,1]时,恒有|
 (x)|≤
(x)|≤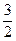 .………………………4分
.………………………4分故有
 ≤
≤ (1)≤
(1)≤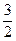 ,
, ≤
≤ (-1)≤
(-1)≤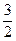 ,
, ≤
≤ (0)≤
(0)≤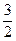 ,………………………5
,………………………5即
 ………6
………6①+②,得
 ≤ab≤
≤ab≤ ,……………………………8分
,……………………………8分又由③,得
ab=
 ,
,将上式代回①和②,得
a+b=0,
故f(x)=x3
 x. ……………………9分
x. ……………………9分(III) 假设
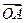 ⊥
⊥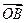 ,
,即
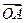
 =
= =" st+f(s)f(t)=0," ……………10分
=" st+f(s)f(t)=0," ……………10分(s-a)(s-b)(t-a)(t-b)=-1,
[st-(s+t)a+a2][st-(s+t)b+b2]="-1," ……………………………………11分
由s,t为
 (x)=0的两根可得,
(x)=0的两根可得,s+t=
 (a+b), st=
(a+b), st=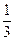 , (0<a<b),
, (0<a<b),从而有ab(a-b)2="9." ……………………………………12分
这样(a+b)2=(a-b)2+4ab
=
 +4ab≥2
+4ab≥2 =12,
=12,即 a+b≥2
 ,
,这样与a+b<2
 矛盾. ……………………13分
矛盾. ……………………13分故
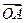 与
与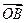 不可能垂直.
不可能垂直.
练习册系列答案
相关题目
 处取得极值.
处取得极值. 上的单调性;
上的单调性;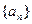 满足
满足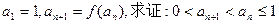 ;
;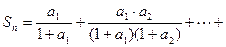
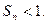
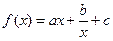 (
(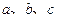 是常数)是奇函数,且满足
是常数)是奇函数,且满足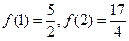 ,
,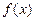 在区间
在区间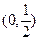 上的单调性并说明理由;
上的单调性并说明理由;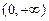 上的最小值.
上的最小值.
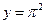 ,则
,则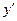 等于( )
等于( )
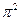
 在y轴上的截距是2,且在
在y轴上的截距是2,且在 上单调递增,在(-1,2)上单调递减.
上单调递增,在(-1,2)上单调递减. ,求
,求 的单调区间.
的单调区间.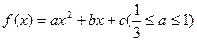 的图象经过A(0,1),且在该点处的切线与直线
的图象经过A(0,1),且在该点处的切线与直线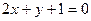 平行.
平行.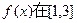 上的最大值与最小值分别为M(a),N(a),求F(a)=M(a)-N(a)的表达式.
上的最大值与最小值分别为M(a),N(a),求F(a)=M(a)-N(a)的表达式.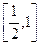 上变化时,证明:
上变化时,证明: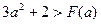
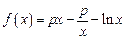 ,
,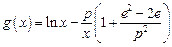 ,其中
,其中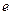 为无理数
为无理数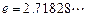 .(1)若
.(1)若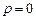 ,求证:
,求证: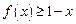 ;(2)若
;(2)若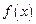 在其定义域内是单调函数,求
在其定义域内是单调函数,求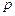 的取值范围;(3)对于区间(1,2)中的任意常数
的取值范围;(3)对于区间(1,2)中的任意常数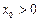 使
使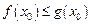 成立?
成立?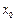 ;否则,说明理由.
;否则,说明理由.
 ,求
,求 .
.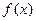 是偶函数,当
是偶函数,当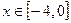 时.
时.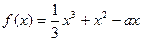 (a为实数).
(a为实数).
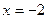 处有极值,求a的值。(6分)
处有极值,求a的值。(6分)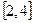 上是减函数,求a的取值范围。(8分)
上是减函数,求a的取值范围。(8分)