题目内容
已知函数f(x)=x3-ax-b (a,b∈R)
(1)当a=b=1时,求函数f(x)的单调区间
(2)是否存在a,b,使得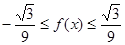 对任意的x∈[0,1]成立?若存在,求出a,b的值,若不存在,说明理由。
对任意的x∈[0,1]成立?若存在,求出a,b的值,若不存在,说明理由。
(1)当a=b=1时,求函数f(x)的单调区间
(2)是否存在a,b,使得
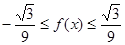 对任意的x∈[0,1]成立?若存在,求出a,b的值,若不存在,说明理由。
对任意的x∈[0,1]成立?若存在,求出a,b的值,若不存在,说明理由。(1)函数f(x)的单调递增区间为( )和(
)和(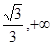 ),函数f(x)的单调递减区间为(
),函数f(x)的单调递减区间为(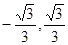 ) (2)存在a=1,
) (2)存在a=1,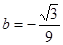
 )和(
)和(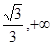 ),函数f(x)的单调递减区间为(
),函数f(x)的单调递减区间为(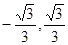 ) (2)存在a=1,
) (2)存在a=1,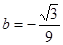
(1)f(x)=x3-x-1, =3x2-1=0,x=
=3x2-1=0,x=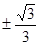 ,x∈(
,x∈( )或x∈(
)或x∈(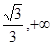 )时
)时 >0,x∈(
>0,x∈(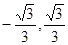 )时
)时 <0,所以函数f(x)的单调递增区间为(
<0,所以函数f(x)的单调递增区间为( )和(
)和(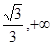 ),函数f(x)的单调递减区间为(
),函数f(x)的单调递减区间为(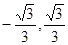 )…5分
)…5分
(2)假设存在这样的a,b,使得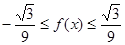 对任意的x∈[0,1]成立,则
对任意的x∈[0,1]成立,则
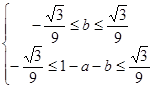 ①,两式相加可得0<
①,两式相加可得0<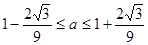 <3,所以函数f(x)在区间[
<3,所以函数f(x)在区间[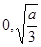 )递减,在区间[
)递减,在区间[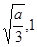 ]递增,所以
]递增,所以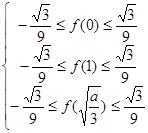 ②,由不等式组中的第二式加第三式可得
②,由不等式组中的第二式加第三式可得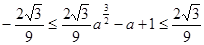 ,由不等式组中的第一式加第三式可得
,由不等式组中的第一式加第三式可得 。 10分
。 10分
记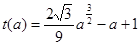 ,
,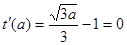 ,a=3,又
,a=3,又 ,
,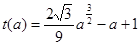 在
在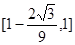 为减函数,又
为减函数,又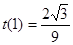 ,所以
,所以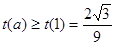 ,所以
,所以 ,所以a=1,代入②式可得
,所以a=1,代入②式可得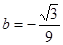 ,所以存在a=1,
,所以存在a=1,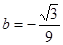 ,使得
,使得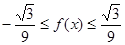 对任意的x∈[0,1]成立。 16分
对任意的x∈[0,1]成立。 16分
 =3x2-1=0,x=
=3x2-1=0,x=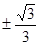 ,x∈(
,x∈( )或x∈(
)或x∈(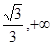 )时
)时 >0,x∈(
>0,x∈(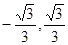 )时
)时 <0,所以函数f(x)的单调递增区间为(
<0,所以函数f(x)的单调递增区间为( )和(
)和(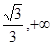 ),函数f(x)的单调递减区间为(
),函数f(x)的单调递减区间为(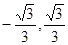 )…5分
)…5分(2)假设存在这样的a,b,使得
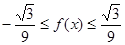 对任意的x∈[0,1]成立,则
对任意的x∈[0,1]成立,则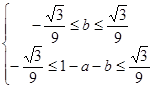 ①,两式相加可得0<
①,两式相加可得0<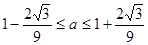 <3,所以函数f(x)在区间[
<3,所以函数f(x)在区间[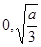 )递减,在区间[
)递减,在区间[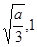 ]递增,所以
]递增,所以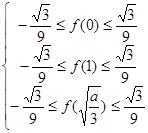 ②,由不等式组中的第二式加第三式可得
②,由不等式组中的第二式加第三式可得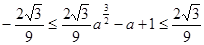 ,由不等式组中的第一式加第三式可得
,由不等式组中的第一式加第三式可得 。 10分
。 10分记
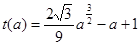 ,
,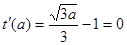 ,a=3,又
,a=3,又 ,
,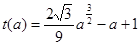 在
在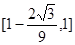 为减函数,又
为减函数,又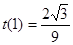 ,所以
,所以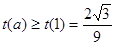 ,所以
,所以 ,所以a=1,代入②式可得
,所以a=1,代入②式可得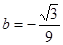 ,所以存在a=1,
,所以存在a=1,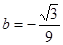 ,使得
,使得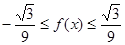 对任意的x∈[0,1]成立。 16分
对任意的x∈[0,1]成立。 16分
练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
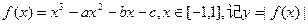 的最大值为M。
的最大值为M。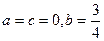 时,求M的值。
时,求M的值。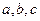 取遍所有实数时,求M的最小值
取遍所有实数时,求M的最小值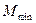 ;
;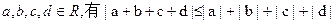 ,当
,当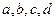 同号时取等号)
同号时取等号)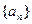 满足
满足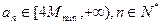 ,求证:
,求证: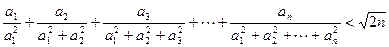 。
。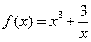 ,求函数f(x)的单调区间及其极值.
,求函数f(x)的单调区间及其极值.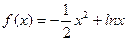 ,
,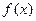 的单调区间;
的单调区间;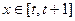
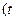 为大于0的常数),求
为大于0的常数),求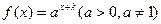 的图象过(-1,1)点,其反函数
的图象过(-1,1)点,其反函数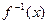 的图象过(8,2)点。
的图象过(8,2)点。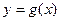 的图象,写出
的图象,写出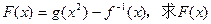 的最小值及取最小值时x的值。
的最小值及取最小值时x的值。 在y轴上的截距是2,且在
在y轴上的截距是2,且在 上单调递增,在(-1,2)上单调递减.
上单调递增,在(-1,2)上单调递减. ,求
,求 的单调区间.
的单调区间.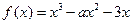 ,
,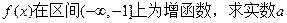 的取值范围;
的取值范围; 的图象与
的图象与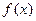 的图象恰有3个交点?若存在求出
的图象恰有3个交点?若存在求出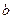 的取值范围;若不存在,试说明理由.
的取值范围;若不存在,试说明理由.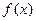 是偶函数,当
是偶函数,当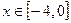 时.
时.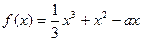 (a为实数).
(a为实数).
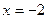 处有极值,求a的值。(6分)
处有极值,求a的值。(6分)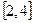 上是减函数,求a的取值范围。(8分)
上是减函数,求a的取值范围。(8分)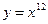 ;(2)
;(2)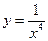 ;(3)
;(3)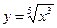 .
.