题目内容
16.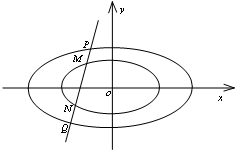 已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个顶点为B(0,1),过焦点且垂直于长轴的弦长为$\sqrt{2}$,直线l交椭圆C1于M,N两点.
已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个顶点为B(0,1),过焦点且垂直于长轴的弦长为$\sqrt{2}$,直线l交椭圆C1于M,N两点.(Ⅰ) 求椭圆C1的方程;
(Ⅱ)若△BMN的重心恰好为椭圆的右焦点F,求直线l的方程;
(Ⅲ)直线l与椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=λ(λ∈R,λ>1)交于P,Q两点(如图),求证|PM|=|NQ|.
分析 (I)由题意,椭圆的焦点在x轴上,利用椭圆的顶点为B(0,1),过焦点且垂直长轴的弦长为$\sqrt{2}$,建立方程组,从而可求椭圆的几何量,即可求椭圆C1的方程;
(Ⅱ)设M(x1,y1),N(x2,y2),又F(1,0),求得△BMN的重心,再由直线方程和椭圆方程联立,运用韦达定理,解方程即可得到直线方程;
(Ⅲ)设直线l:y=kx+t,分别代入椭圆C1,C2的方程,运用韦达定理,结合中点坐标公式,可得MN和PQ的中点重合,即可得证.
解答 解:(Ⅰ)由题意,椭圆的焦点在x轴上,
可得$\left\{\begin{array}{l}{b=1}\\{\frac{2{b}^{2}}{a}=\sqrt{2}}\end{array}\right.$,∴a=$\sqrt{2}$,b=1,c=$\sqrt{{a}^{2}-{b}^{2}}$=1,
∴椭圆C1的方程为$\frac{{x}^{2}}{2}$+y2=1;
(Ⅱ)设M(x1,y1),N(x2,y2),又F(1,0),
则△BMN的重心为($\frac{{x}_{1}+{x}_{2}+0}{3}$,$\frac{{y}_{1}+{y}_{2}+1}{3}$),
由题意可得x1+x2=3,y1+y2=-1,
设直线l:y=kx+t,代入椭圆C1的方程,可得
(1+2k2)x2+4ktx+2t2-2=0,
即有x1+x2=-$\frac{4kt}{1+2{k}^{2}}$,
即4kt=-3(1+2k2),
又k(x1+x2)+2t=-1,即有$\frac{-4k{t}^{2}}{1+2{k}^{2}}$+2t=-1,
解得k=$\frac{3}{2}$,t=-$\frac{11}{4}$,
代入判别式(4kt)2-4(1+2k2)(2t2-2)>0成立,
即有直线l的方程为y=$\frac{3}{2}$x-$\frac{11}{4}$;
(Ⅲ)证明:设直线l:y=kx+t,代入椭圆C1的方程,可得
(1+2k2)x2+4ktx+2t2-2=0,
设M(x1,y1),N(x2,y2),
即有x1+x2=-$\frac{4kt}{1+2{k}^{2}}$,
则有MN的中点的横坐标为-$\frac{2kt}{1+2{k}^{2}}$;
设直线l:y=kx+t,代入椭圆C2:$\frac{{x}^{2}}{2}$+y2=λ的方程,可得
(1+2k2)x2+4ktx+2t2-2λ=0,
设P(x3,y3),Q(x4,y4),
即有x3+x4=-$\frac{4kt}{1+2{k}^{2}}$,
则有PQ的中点的横坐标为-$\frac{2kt}{1+2{k}^{2}}$.
即有MN和PQ的中点重合,
即有|PM|=|NQ|.
点评 本题考查椭圆的方程和性质,主要考查直线方程和椭圆方程联立,运用韦达定理,以及中点坐标公式,考查运算求解能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案 如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,且AC=BC=CC1=2,M是AB1与A1B的交点,N是B1C1的中点.
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,且AC=BC=CC1=2,M是AB1与A1B的交点,N是B1C1的中点.(Ⅰ)求证:MN∥平面ACC1A1;
(Ⅱ)求三棱锥N-A1BC的体积.
| A. | $\frac{1}{4}:\frac{1}{6}:\frac{1}{π}$ | B. | $\frac{π}{6}:\frac{π}{4}$:2 | C. | 2:3:2π | D. | $\frac{π}{6}:\frac{π}{4}$:1 |
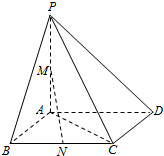 如图,四棱锥P-ABCD中,PA=AB=1,PA⊥底面ABCD,底面ABCD为正方形,且M,N分别为PA与BC的中点
如图,四棱锥P-ABCD中,PA=AB=1,PA⊥底面ABCD,底面ABCD为正方形,且M,N分别为PA与BC的中点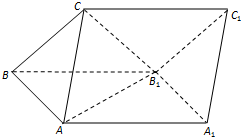 如图,三棱柱ABC-A1B1C1的侧面ABB1A1为正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C.
如图,三棱柱ABC-A1B1C1的侧面ABB1A1为正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C.