题目内容
5．
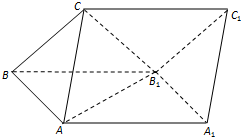如图，三棱柱ABC-A1B1C1的侧面ABB1A1为正方形，侧面BB1C1C为菱形，∠CBB1=60°，AB⊥B1C．（Ⅰ）求证：平面ABB1A1⊥BB1C1C；
（Ⅱ）若AB=2，求三棱柱ABC-A1B1C1体积．
分析 （I）证AB垂直于平面内的两条相交直线，再由线面垂直⇒面面垂直；
（II）先求得三棱锥B1-ABC的体积，再利用棱柱是由三个体积相等的三棱锥组合而成来求解．
解答 
（Ⅰ）证明：由侧面ABB1A1为正方形，知AB⊥BB1．
又AB⊥B1C，BB1∩B1C=B1，所以AB⊥平面BB1C1C，
又AB?平面ABB1A1，所以平面ABB1A1⊥BB1C1C．…（4分）
（Ⅱ）解：设O是BB1的中点，连结CO，则CO⊥BB1．
由（Ⅰ）知，CO⊥平面ABB1A1，且CO=$\frac{\sqrt{3}}{2}$BC=$\frac{\sqrt{3}}{2}$AB=$\sqrt{3}$．
连结AB1，
则${V}_{C-AB{B}_{1}}$=$\frac{1}{3}$${S}_{△AB{B}_{1}}$•CO=$\frac{1}{6}$AB2•CO=$\frac{2\sqrt{3}}{3}$．…（8分）
因${V}_{{B}_{1}-ABC}$=${V}_{C-AB{B}_{1}}$=$\frac{1}{3}$${V}_{ABC-{A}_{1}{B}_{1}{C}_{1}}$=$\frac{2\sqrt{3}}{3}$，
故三棱柱ABC-A1B1C1的体积${V}_{ABC-{A}_{1}{B}_{1}{C}_{1}}$=2$\sqrt{3}$．…（12分）．
点评 本题考查面面垂直的判定及空间几何体的体积，考查学生分析解决问题的能力，正确运用线面垂直的判定是关键．
练习册系列答案
相关题目
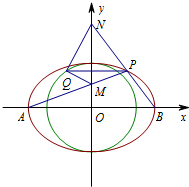已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）上的点到它的两个焦点的距离之和为4，以椭圆C的短轴为直径的圆O经过这两个焦点，点A，B分别是椭圆C的左、右顶点．
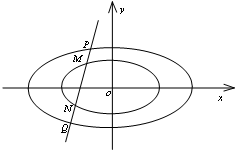已知椭圆C1：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的一个顶点为B（0，1），过焦点且垂直于长轴的弦长为$\sqrt{2}$，直线l交椭圆C1于M，N两点．