题目内容
4.已知函数f(x)=$\frac{1}{x}+m\sqrt{x}$(m∈R),若f(x)在x=4处的切线与直线16x+7y=0垂直.(Ⅰ)求m的值;
(Ⅱ)令g(x)=kxex,对?x1∈(0,+∞),?x2∈(0,1),总有f(x1)≥g(x2),求实数k的取值范围.
分析 (Ⅰ)求导数,利用f(x)在x=4处的切线与直线16x+7y=0垂直,可得f′(4)=-$\frac{1}{16}$+$\frac{m}{4}$=$\frac{7}{16}$,即可求m的值;
(Ⅱ)对?x1∈(0,+∞),?x2∈(0,1),总有f(x1)≥g(x2),可得f(x)min≥g(x)max,分类讨论,即可得出结论.
解答 解:(Ⅰ)f′(x)=-$\frac{1}{{x}^{2}}$+$\frac{m}{2\sqrt{x}}$
∵f(x)在x=4处的切线与直线16x+7y=0垂直,
∴f′(4)=-$\frac{1}{16}$+$\frac{m}{4}$=$\frac{7}{16}$,
∴m=2;
(Ⅱ)∵对?x1∈(0,+∞),?x2∈(0,1),总有f(x1)≥g(x2),
∴f(x)min≥g(x)max,
∵f′(x)=$\frac{(\sqrt{x}-1)(x+\sqrt{x}+1)}{{x}^{2}}$,
∴x∈(0,1),f′(x)<0,f(x)单调递增,x∈(1,+∞),f′(x)>0,f(x)单调递减,
∴f(x)min=f(1)=3,
g′(x)=k(ex+xex),
k>0,x∈(0,1),g′(x)>0,g(x)单调递增,3≥g(x)max=ke,∴k≤$\frac{3}{e}$;
k<0,x∈(0,1),g′(x)<0,g(x)单调递减,3≥g(x)max=0,∴k<0;
k=0,3>g(x)max=0,
∴k≤$\frac{3}{e}$.
点评 本题考查导数知识的综合运用,考查导数的几何意义,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
2.在△ABC中,角A、B、C的对边分别为a,b,c,且满足$\sqrt{2}$acosB=bcosC+ccosB,则角B的大小为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
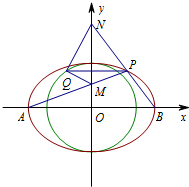 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)上的点到它的两个焦点的距离之和为4,以椭圆C的短轴为直径的圆O经过这两个焦点,点A,B分别是椭圆C的左、右顶点.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)上的点到它的两个焦点的距离之和为4,以椭圆C的短轴为直径的圆O经过这两个焦点,点A,B分别是椭圆C的左、右顶点. 设椭圆中心在坐标原点,A(4,0),B(0,2)是它的两个顶点,直线y=kx(k>0)与AB相交于点D,与椭圆相交于E、F两点.
设椭圆中心在坐标原点,A(4,0),B(0,2)是它的两个顶点,直线y=kx(k>0)与AB相交于点D,与椭圆相交于E、F两点.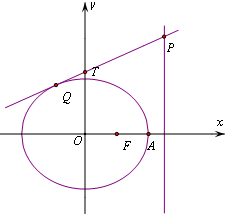 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{1}{2}$,右焦点为F,右顶点为A,P为直线x=$\frac{5}{4}$a上的任意一点,且($\overrightarrow{PF}$+$\overrightarrow{PA}$)•$\overrightarrow{AF}$=2.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{1}{2}$,右焦点为F,右顶点为A,P为直线x=$\frac{5}{4}$a上的任意一点,且($\overrightarrow{PF}$+$\overrightarrow{PA}$)•$\overrightarrow{AF}$=2.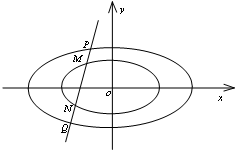 已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个顶点为B(0,1),过焦点且垂直于长轴的弦长为$\sqrt{2}$,直线l交椭圆C1于M,N两点.
已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个顶点为B(0,1),过焦点且垂直于长轴的弦长为$\sqrt{2}$,直线l交椭圆C1于M,N两点.