��Ŀ����
11����Ԫǰ3���ͣ���ϣ��ŷ������ڡ�����ԭ���������������������V��������ֱ����D�������������ȡ����˼�V=kD3��ŷ�����δ����k��ֵ.17�����ձ���ѧ���Ƕ����������ķ��������˽⣬���ǽ������ʽV=kD3�еij���k��Ϊ����Բ�ʡ�������ʡ������Ƶأ����ڵȱ�Բ����������������ε�Բ������������Ҳ�����ù�ʽV=kD3��������ڵȱ�Բ���У�D��ʾ����Բ��ֱ�������������У�D��ʾ�ⳤ�����������ô������ʽ�����ֱ��Ϊa�����ȱ�Բ��������Բ��ֱ��Ϊa���������壨�ⳤΪa���ġ�����ʡ��ֱ�Ϊk1��k2��k3����ôk1��k2��k3��������| A�� | $\frac{1}{4}��\frac{1}{6}��\frac{1}{��}$ | B�� | $\frac{��}{6}��\frac{��}{4}$��2 | C�� | 2��3��2�� | D�� | $\frac{��}{6}��\frac{��}{4}$��1 |
���� ������Բ�����������������㹫ʽ������������ɵó���
��� �⣺��${V_1}=\frac{4}{3}��{R^3}=\frac{4}{3}��{��\frac{a}{2}��^3}=\frac{��}{6}{a^3}⇒{k_1}=\frac{��}{6}$��
${V_2}=��{R^2}a=��{��\frac{a}{2}��^2}a=\frac{��}{4}{a^3}⇒{k_2}=\frac{��}{4}$��
${V_3}={a^3}⇒{k_3}=1$��
��${k_1}��{k_2}��{k_3}=\frac{��}{6}��\frac{��}{4}��1$��
���� ���⿼������Բ�����������������㹫ʽ����������������е��⣮

��ϰ��ϵ�д�
 ���ɶ��ȫ���ƿؾ�ϵ�д�
���ɶ��ȫ���ƿؾ�ϵ�д�
�����Ŀ
 ����ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��������e=$\frac{1}{2}$����M����ԲC�ϣ���M����ԲC����������ľ���֮����4��
����ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��������e=$\frac{1}{2}$����M����ԲC�ϣ���M����ԲC����������ľ���֮����4��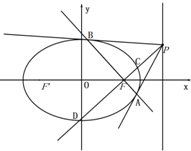 ��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{1}{2}$����ԭ��ΪԲ�ģ�����Բ�Ķ̰���Ϊ�뾶��Բ��ֱ��x-y+$\sqrt{6}$=0���У�
��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{1}{2}$����ԭ��ΪԲ�ģ�����Բ�Ķ̰���Ϊ�뾶��Բ��ֱ��x-y+$\sqrt{6}$=0���У�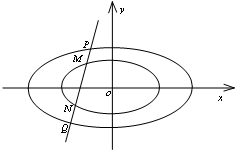 ��֪��ԲC1��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����һ������ΪB��0��1�����������Ҵ�ֱ�ڳ�����ҳ�Ϊ$\sqrt{2}$��ֱ��l����ԲC1��M��N���㣮
��֪��ԲC1��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����һ������ΪB��0��1�����������Ҵ�ֱ�ڳ�����ҳ�Ϊ$\sqrt{2}$��ֱ��l����ԲC1��M��N���㣮