题目内容
1.已知数列{an}满足$\frac{{a}_{n+1}+{a}_{n}-1}{{a}_{n+1}-{a}_{n}+1}$=n(n∈N*),且a4=28,则首项a1=1,通项公式an=(2n-1)n.分析 根据数列的递推关系,进行转化变形,构造等差数列即可得到结论.
解答 解:由$\frac{{a}_{n+1}+{a}_{n}-1}{{a}_{n+1}-{a}_{n}+1}$=n(n∈N*),得an+1+an-1=nan+1-nan+n,
即(1-n)an+1+(1+n)an=1+n,
an+1=$\frac{n+1}{n-1}$an-$\frac{n+1}{n-1}$an=$\frac{1}{n-1}$(an-1)×(n+1),
即$\frac{{a}_{n+1}}{n+1}$=$\frac{1}{n-1}$•an-$\frac{1}{n-1}$=$\frac{n}{n-1}$•$\frac{{a}_{n}}{n}$-$\frac{n}{n-1}$•$\frac{1}{n}$,
则$\frac{{a}_{n+1}}{n+1}$-1=$\frac{n}{n-1}$•($\frac{{a}_{n}}{n}$-1),
即$\frac{1}{n}$•($\frac{{a}_{n+1}}{n+1}$-1)=$\frac{1}{n-1}$•($\frac{{a}_{n}}{n}$-1),
即{$\frac{1}{n-1}$•($\frac{{a}_{n}}{n}$-1)}为常数列,
∵a4=28,
∴$\frac{1}{n-1}$•($\frac{{a}_{n}}{n}$-1)=$\frac{1}{4-1}•(\frac{{a}_{4}}{4}-1)$=$\frac{1}{3}•(\frac{28}{4}-1)$=$\frac{1}{3}×6=2$,
即$\frac{1}{n-1}$•($\frac{{a}_{n}}{n}$-1)=2,
整理得an=(2n-1)n,则a2=6,
当n=1时,$\frac{{a}_{2}+{a}_{1}-1}{{a}_{2}-{a}_{1}+1}=1$,即a2+a1-1=a2-a1+1,
即a1=1,满足an=(2n-1)n,
故通项公式an=(2n-1)n,
故答案为:1,(2n-1)n
点评 本题目主要考查了利用数列的递推公式求解数列的通项公式,解题得关键是利用递推公式构造特殊数列.综合性较强,难度较大.

 阅读快车系列答案
阅读快车系列答案| A. | -4 | B. | 3 | C. | 3或-4 | D. | ±4 |
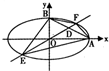 设椭圆中心在坐标原点,A(4,0),B(0,2)是它的两个顶点,直线y=kx(k>0)与AB相交于点D,与椭圆相交于E、F两点.
设椭圆中心在坐标原点,A(4,0),B(0,2)是它的两个顶点,直线y=kx(k>0)与AB相交于点D,与椭圆相交于E、F两点.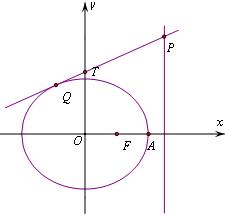 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{1}{2}$,右焦点为F,右顶点为A,P为直线x=$\frac{5}{4}$a上的任意一点,且($\overrightarrow{PF}$+$\overrightarrow{PA}$)•$\overrightarrow{AF}$=2.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{1}{2}$,右焦点为F,右顶点为A,P为直线x=$\frac{5}{4}$a上的任意一点,且($\overrightarrow{PF}$+$\overrightarrow{PA}$)•$\overrightarrow{AF}$=2.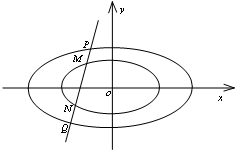 已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个顶点为B(0,1),过焦点且垂直于长轴的弦长为$\sqrt{2}$,直线l交椭圆C1于M,N两点.
已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个顶点为B(0,1),过焦点且垂直于长轴的弦长为$\sqrt{2}$,直线l交椭圆C1于M,N两点.