题目内容

6．已知$sin\frac{α}{2}=\frac{2}{3}$，则cos（π-α）=-$\frac{1}{9}$．

分析 由诱导公式及二倍角的余弦函数公式即可得解．

解答 解：∵$sin\frac{α}{2}=\frac{2}{3}$，
∴cos（π-α）=-cosα=-（1-2sin2$\frac{α}{2}$）=-$\frac{1}{9}$．
故答案为：-$\frac{1}{9}$．

点评 本题主要考查了诱导公式及二倍角的余弦函数公式的应用，属于基础题．

练习册系列答案
相关题目
4．以极点为原点，极轴为x轴正半轴，建立平面直角坐标系，两坐标系中取相同的长度单位，圆O1的方程为ρ=4cosθ，圆O2的参数方程为$\left\{\begin{array}{l}{x=2cosθ}\\{y=-2+2sinθ}\end{array}\right.$（θ为参数），
（1）求两圆的一般方程．
（2）求两圆的公共弦的长度．
5．当-1＜m＜1时，复数z=$\frac{-1+i}{m+i}$（i为虚数单位）在复平面内对应的点位于（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
2．在△ABC中，角A、B、C的对边分别为a，b，c，且满足$\sqrt{2}$acosB=bcosC+ccosB，则角B的大小为（　　）
A．$\frac{π}{6}$B．$\frac{π}{4}$C．$\frac{π}{3}$D．$\frac{π}{2}$
1．已知F1，F2分别为椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）左、右焦点，点P（1，y0）在椭圆上，且PF2⊥x轴，△PF1F2的周长为6；
（1）求椭圆的标准方程；
（2）E、F是曲线C上异于点P的两个动点，如果直线PE与直线PF的倾斜角互补，证明：直线EF的斜率为定值，并求出这个定值．
11．已知f（x）=2sin（x-$\frac{π}{6}$）cos（x-$\frac{π}{6}$）+2．
（Ⅰ）求函数f（x）的最小正周期；
（Ⅱ）求函数f（x）的对称轴和对称中心．
18．如图所示，AB是半径为1的圆的直径，过点A，B分别引弦AD和BE，相交于点C，过点C作CF⊥AB，垂足为点F．已知∠CAB=30°，∠DCB=60°．
（1）求∠EAB的大小；
（2）求AC•AD+BC•BE的值．
15．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）上的点到它的两个焦点的距离之和为4，以椭圆C的短轴为直径的圆O经过这两个焦点，点A，B分别是椭圆C的左、右顶点．
（Ⅰ）求圆O和椭圆C的方程；
（Ⅱ）已知P，Q分别是椭圆C和圆O上的动点（P，Q位于y轴两侧），且直线PQ与x轴平行，直线AP，BP分别与y轴交于点M，N．求证：∠MQN为定值．
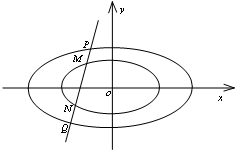16．已知椭圆C1：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的一个顶点为B（0，1），过焦点且垂直于长轴的弦长为$\sqrt{2}$，直线l交椭圆C1于M，N两点．
（Ⅰ） 求椭圆C1的方程；
（Ⅱ）若△BMN的重心恰好为椭圆的右焦点F，求直线l的方程；
（Ⅲ）直线l与椭圆C2：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=λ（λ∈R，λ＞1）交于P，Q两点（如图），求证|PM|=|NQ|．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网