题目内容
【题目】某学校为调查高二年级学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图(1))和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高(单位:
)在
内的男生人数有16人.
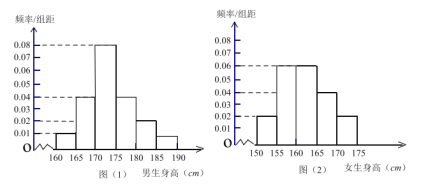
(Ⅰ)求在抽取的学生中,男女生各有多少人?
(Ⅱ)根据频率分布直方图,完成下列的
列联表,并判断能有多大(百分之几)的把握认为“身高与性别有关”?
|
| 总计 | |
男生人数 | |||
女生人数 | |||
总计 |
附:参考公式和临界值表:
,
| 5.024 | 6.635 | 7.879 | 10.828 |
| 0.025 | 0.010 | 0.005 | 0.001 |
【答案】(Ⅰ) 男生40人，女生40人；(Ⅱ) 表格见解析，有
的把握认为身高与性别有关.
【解析】
(Ⅰ)根据题目直方图中，因为身高在
的男生的频率为
，人数为16人，可得男生的总人数，进而求得女生的人数；
(Ⅱ) 分别计算男生、女生身高
的人数，完成列联表，代入公式并分析临界值表即可得到结论.
(Ⅰ)直方图中，因为身高在170~175cm的男生的频率为，
设男生数为
，则
，得
，
由男生的人数为40，得女生的人数为
.
(Ⅱ) 男生身高的人数
，
女生身高的人数
，所以可得到下列列联表：
|
| 总计 | |
男生人数 | 30 | 10 | 40 |
女生人数 | 4 | 36 | 40 |
总计 | 34 | 46 | 80 |
，
所以能有的把握认为身高与性别有关.
【题目】某快递公司收取快递费用的标准是：重量不超过
的包裹收费
元；重量超过
的包裹，除
收费
元之外，超过
的部分，每超出
（不足
，按
计算）需再收
元.该公司将最近承揽的
件包裹的重量统计如下：
包裹重量（单位： |
|
|
|
|
|
包裹件数 |
|
|
|
|
|
公司对近
天，每天揽件数量统计如下表：
包裹件数范围 |
|
|
|
|
|
包裹件数 （近似处理） |
|
|
|
|
|
天数 |
|
|
|
|
|
以上数据已做近似处理，并将频率视为概率.
（1）计算该公司未来
天内恰有
天揽件数在
之间的概率；
（2）（i）估计该公司对每件包裹收取的快递费的平均值；
（ii）公司将快递费的三分之一作为前台工作人员的工资和公司利润，剩余的用作其他费用.目前前台有工作人员
人，每人每天揽件不超过
件，工资
元.公司正在考虑是否将前台工作人员裁减
人，试计算裁员前后公司每日利润的数学期望，并判断裁员是否对提高公司利润更有利？
