题目内容
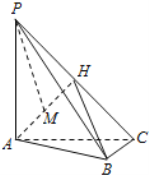
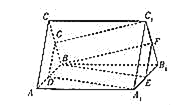
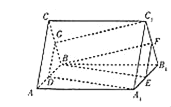
【题目】如图所示,三棱柱ABC﹣A1B1C1的侧棱垂直于底面,且底面是边长为2的正三角形,AA1=3,点D,E,F,G分别是所在棱的中点.
(Ⅰ)证明:平面BEF∥平面DA1C1;
(Ⅱ)求三棱柱ABC﹣A1B1C1夹在平面BEF和平面DA1C1之间的部分的体积.
附:台体的体积![]() ,其中S和S′分别是上、下底面面积,h是台体的高.
,其中S和S′分别是上、下底面面积,h是台体的高.
【答案】(Ⅰ)见解析(Ⅱ)![]()
【解析】
(Ⅰ)分别证明EF∥平面DA1C1和BE∥平面DA1C1,即可得证;
(Ⅱ)可看作三棱台DBG﹣A1B1C1减掉三棱锥B﹣B1EF剩余部分,分别计算,求差即可.
证明:(Ⅰ)∵E,F分别是A1 B1和B1C1的中点,∴EF∥A1C1,
∵EF平面DA1C1,A1C1平面DA1C1,
∴EF∥平面DA1C1,
∵D,E分别是AB和A1B1的中点,∴![]() ,
,
∴四边形BDA1E是平行四边形,∴BE∥A1D,
∵BE 平面DA1C1,A1D 平面DA1C1,
∴BE∥平面DA1C1,
∵BE∩EF=E,∴平面BEF∥平面DA1C1.
(Ⅱ)由图可知,三棱柱ABC﹣A1B1C1夹在平面BEF和平面DA1C1之间的部分,
可看作三棱台DBG﹣A1B1C1减掉三棱锥B﹣B1EF剩余部分,
∵三棱柱ABC﹣A1B1C1夹在平面BEF和平面DA1C1之间的部分的体积.
![]() ,
,
∴三棱台DBG﹣A1B1C1的体积为:![]() ,
,
三棱锥B﹣B1EF体积![]() ,
,
∴三棱柱ABC﹣A1B1C1夹在平面BEF和平面DA1C1之间的部分的体积:![]() .
.

【题目】某学校为调查高二年级学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图(1))和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高(单位:![]() )在
)在![]() 内的男生人数有16人.
内的男生人数有16人.
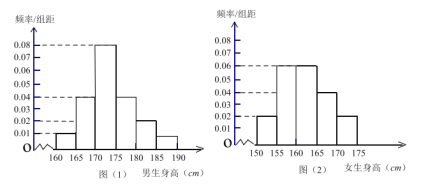
(Ⅰ)求在抽取的学生中,男女生各有多少人?
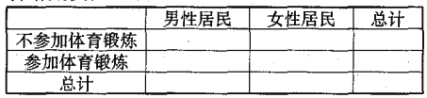
(Ⅱ)根据频率分布直方图,完成下列的![]() 列联表,并判断能有多大(百分之几)的把握认为“身高与性别有关”?
列联表,并判断能有多大(百分之几)的把握认为“身高与性别有关”?
|
| 总计 | |
男生人数 | |||
女生人数 | |||
总计 |
附:参考公式和临界值表:
 ,
,
| 5.024 | 6.635 | 7.879 | 10.828 |
| 0.025 | 0.010 | 0.005 | 0.001 |