已知复数z=$\frac{-1-2i}{{{{(1+i)}^2}}}$.则$\overline z$=( )A．-$\frac{3}{4}+\frac{1}{4}$iB．-$\frac{1}{4}+\frac{3}{4}$iC．-1+$\frac{1}{2}$iD．-1-$\frac{1}{2}$i 题目和参考答案——青夏教育精英家教网—

题目内容

18．已知复数z=$\frac{-1-2i}{{{{（1+i）}^2}}}$，则$\overline z$=（　　）

A．

-$\frac{3}{4}+\frac{1}{4}$i

B．

-$\frac{1}{4}+\frac{3}{4}$i

C．

-1+$\frac{1}{2}$i

D．

-1-$\frac{1}{2}$i

分析利用复数的运算法则、共轭复数的定义即可得出．

解答解：复数z=$\frac{-1-2i}{{{{（1+i）}^2}}}$=$\frac{-1-2i}{2i}$=$\frac{（1+2i）•i}{-2i•i}$=$\frac{-2+i}{2}$，则$\overline z$=-1-$\frac{1}{2}$i．
故选：D．

点评本题考查了复数的运算法则、共轭复数的定义，属于基础题．

练习册系列答案

9．已知函数f（x）=$\left\{{\begin{array}{l}{x+\frac{1}{x}，x＞0}\\{{x^3}+3，x≤0}\end{array}}$，当2＜a≤3时，则方程f（2x²+x）=a的根最多个数是（　　）

6．已知集合$A=\left\{{x\left|{y=\sqrt{1-x}}\right.}\right\}$，B={x|1≤3^x≤9}，则A∩B=（　　）

13．

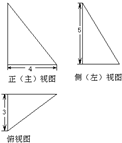
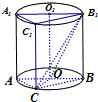如图，圆柱OO₁内接直三棱柱ABC-A₁B₁C₁，该三棱柱的底面为圆柱底面的内接三角形，且AB是圆O的直径，且AB=AA₁．在圆柱OO₁内随机选取一点，记该点取自于三棱柱ABC-A₁B₁C₁内的概率为P
（1）当点C在圆周上运动时，求P的最大值；
（2）记平面A₁ACC₁与平面B₁OC所成的角为θ（0°＜θ≤90°），当P取最大值时，求sinθ的值．

3．

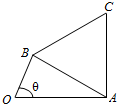已知函数f（x）=sinωx（0＜ω＜2）在区间，[0，$\frac{π}{3}$]上单调递增，在区间[$\frac{π}{3}$，$\frac{2π}{3}$]单调递减；如图，四边形OACB中，a，b，c为△ABC的内角A，B，C的对边，且满足$\frac{sinB+sinC}{sinA}$=$\frac{\frac{4ω}{3}-cosB-cosC}{cosA}$．
（1）证明：b+c=2a；
（2）若b=c，设∠AOB=θ，（0＜θ＜π），OA=2OB=2，求四边形OACB面积的最大值．

10．已知正实数a，b满足：a+b=2．
（Ⅰ）求$\frac{1}{a}+\frac{1}{b}$的最小值m；
（Ⅱ）设函数f（x）=|x-t|+|x+$\frac{1}{t}$|（t≠0），对于（Ⅰ）中求得的m，是否存在实数x，使得f（x）=m成立，若存在，求出x的取值范围，若不存在，说明理由．

7．已知向量$\overrightarrow{a}=（{e}^{x}，1）$，向量$\overrightarrow{b}=（1，x-1）$，设函数f（x）=$\overrightarrow{a}•\overrightarrow{b}$，则函数f（x）的零点个数为（　　）

8．双曲线C：$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点为F，直线l过焦点F，且斜率为k，则直线l与双曲线C的左、右两支都相交的充要条件是（　　）

k＞$\frac{b}{a}$或k＜-$\frac{b}{a}$

D．

-$\frac{b}{a}$＜k＜$\frac{b}{a}$

试题分类