题目内容
10.已知正实数a,b满足:a+b=2.(Ⅰ)求$\frac{1}{a}+\frac{1}{b}$的最小值m;
(Ⅱ)设函数f(x)=|x-t|+|x+$\frac{1}{t}$|(t≠0),对于(Ⅰ)中求得的m,是否存在实数x,使得f(x)=m成立,若存在,求出x的取值范围,若不存在,说明理由.
分析 (1)由题意可得$\frac{1}{a}+\frac{1}{b}$=$\frac{1}{2}$($\frac{1}{a}+\frac{1}{b}$)(a+b)=$\frac{1}{2}$(2+$\frac{b}{a}$+$\frac{a}{b}$),由基本不等式可得;
(2)由不等式的性质可得f(x)≥|x-t-x-$\frac{1}{t}$|=|t+$\frac{1}{t}$|=2,由基本不等式和不等式的性质可得.
解答 解:(1)∵正实数a,b满足a+b=2.
∴$\frac{1}{a}+\frac{1}{b}$=$\frac{1}{2}$($\frac{1}{a}+\frac{1}{b}$)(a+b)
=$\frac{1}{2}$(2+$\frac{b}{a}$+$\frac{a}{b}$)≥$\frac{1}{2}$(2+2$\sqrt{\frac{b}{a}•\frac{a}{b}}$)=2,
当且仅当$\frac{b}{a}$=$\frac{a}{b}$即a=b=1时取等号,
∴$\frac{1}{a}+\frac{1}{b}$的最小值m=2;
(2)由不等式的性质可得f(x)=|x-t|+|x+$\frac{1}{t}$|
≥|x-t-x-$\frac{1}{t}$|=|t+$\frac{1}{t}$|=2
当且仅当t=±1等号时成立,此时-1≤x≤1,
∴存在x∈[-1,1]使f(x)=m成立.
点评 本题考查基本不等式,属基础题.

练习册系列答案
相关题目
20.已知函数f(x)=cos2x-$\frac{1}{2}$,则( )
| A. | f(x)为偶函数且最小正周期为π | B. | f(x)为奇函数且最小正周期为π | ||
| C. | f(x)为偶函数且最小正周期为2π | D. | f(x)为奇函数且最小正周期为2π |
18.已知复数z=$\frac{-1-2i}{{{{(1+i)}^2}}}$,则$\overline z$=( )
| A. | -$\frac{3}{4}+\frac{1}{4}$i | B. | -$\frac{1}{4}+\frac{3}{4}$i | C. | -1+$\frac{1}{2}$i | D. | -1-$\frac{1}{2}$i |
5.已知平面α⊥β,α∩β=m,n?β,则“n⊥m”是“n⊥α”成立的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
19.已知命题p:?x∈R,ex>0命题q:?x∈R,x-2>x2,则( )
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∧(?q)是真命题 | D. | 命题p∨(?q)是假命题 |
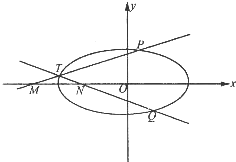 如图所示,椭圆C的离心率为$\frac{\sqrt{3}}{2}$,以坐标原点O为圆心,椭圆C的短半轴长为半径的圆与直线y=$\sqrt{3}$x+2相切.
如图所示,椭圆C的离心率为$\frac{\sqrt{3}}{2}$,以坐标原点O为圆心,椭圆C的短半轴长为半径的圆与直线y=$\sqrt{3}$x+2相切.