题目内容
7．已知向量$\overrightarrow{a}=（{e}^{x}，1）$，向量$\overrightarrow{b}=（1，x-1）$，设函数f（x）=$\overrightarrow{a}•\overrightarrow{b}$，则函数f（x）的零点个数为（ ）| A． | 1 个 | B． | 2 个 | C． | 3 个 | D． | 4 个 |
分析 由数量积得到函数f（x），求导判断其单调性，再由f（0）=0得答案．
解答 解：由向量$\overrightarrow{a}=（{e}^{x}，1）$，向量$\overrightarrow{b}=（1，x-1）$，
得f（x）=$\overrightarrow{a}•\overrightarrow{b}$=ex+x-1，
∵f′（x）=ex+1＞0，∴f（x）为实数集上的增函数，
又f（0）=e0+0-1=0，
∴函数f（x）的零点个数为1个．
故选：A．
点评 本题考查平面向量的数量积运算，考查了函数零点的判断，是基础题．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
17．已知命题p：?x∈R，x-2＞0，命题q：?x∈R，2x＞x2，则下列说法中正确的是（ ）
| A． | 命题p∨q是假命题 | B． | 命题p∧q是真命题 | ||
| C． | 命题p∧（￢q）是真命题 | D． | 命题p∨（￢q）是假命题 |
18．已知复数z=$\frac{-1-2i}{{{{（1+i）}^2}}}$，则$\overline z$=（ ）
| A． | -$\frac{3}{4}+\frac{1}{4}$i | B． | -$\frac{1}{4}+\frac{3}{4}$i | C． | -1+$\frac{1}{2}$i | D． | -1-$\frac{1}{2}$i |
12．在复平面上，复数z=a+bi（a，b∈R）与复数i（i-2）关于实轴对称，则a+b的值为（ ）
| A． | 1 | B． | -3 | C． | 3 | D． | 2 |
19．已知命题p：?x∈R，ex＞0命题q：?x∈R，x-2＞x2，则（ ）
| A． | 命题p∨q是假命题 | B． | 命题p∧q是真命题 | ||
| C． | 命题p∧（?q）是真命题 | D． | 命题p∨（?q）是假命题 |
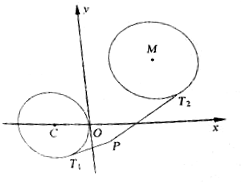设圆C：（x+4）2+y2=16，动圆M：x2+y2-2ax-2（8-a）y+4a+22=0，平面内是还有存在定点P，过点P作圆C的一条切线，切点为T1，过点P作圆M的一条切线，切点为T2，使无穷多个圆M，满足$\frac{P{T}_{1}}{P{T}_{2}}$=$\frac{1}{2}$？如果存在，求出所有这样的点P；如果不存在，请说明理由．