题目内容
8.双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F,直线l过焦点F,且斜率为k,则直线l与双曲线C的左、右两支都相交的充要条件是( )| A. | k>-$\frac{b}{a}$ | B. | k<$\frac{b}{a}$ | C. | k>$\frac{b}{a}$或k<-$\frac{b}{a}$ | D. | -$\frac{b}{a}$<k<$\frac{b}{a}$ |
分析 设直线方程为:y=k(x-c)代入双曲线方程得:(b2-a2k2)x2+2a2k2cx-a2k2c2-a2b2=0,方程有两根,x1•x2=(-a2k2c2-a2b2)÷(b2-a2k2)<0,因-a2k2c2-a2b2必定小于0,故只需:b2-a2k2>0即可,由此能求出结果.
解答 解:由题意可设直线方程为:y=k(x-c)代入双曲线方程得:
(b2-a2k2)x2+2a2k2cx-a2k2c2-a2b2=0,方程有两根,可设为x1>0,x2<0:
x1•x2=(-a2k2c2-a2b2)÷(b2-a2k2)<0,
因-a2k2c2-a2b2必定小于0,故只需:b2-a2k2>0即可,
所以-$\frac{b}{a}$<k<$\frac{b}{a}$
反之当-$\frac{b}{a}$<k<$\frac{b}{a}$时,直线l与双曲线C的左右两支都相交,
故直线l与双曲线C的左右两支都相交的充要条件是-$\frac{b}{a}$<k<$\frac{b}{a}$,
故选:D.
点评 本题考查必要条件、充分条件、充要条件的判断和应用,解题时要认真审题,注意双曲线的性质的灵活运用.

练习册系列答案
相关题目
18.已知复数z=$\frac{-1-2i}{{{{(1+i)}^2}}}$,则$\overline z$=( )
| A. | -$\frac{3}{4}+\frac{1}{4}$i | B. | -$\frac{1}{4}+\frac{3}{4}$i | C. | -1+$\frac{1}{2}$i | D. | -1-$\frac{1}{2}$i |
19.已知命题p:?x∈R,ex>0命题q:?x∈R,x-2>x2,则( )
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∧(?q)是真命题 | D. | 命题p∨(?q)是假命题 |
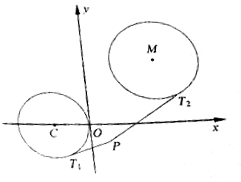 设圆C:(x+4)2+y2=16,动圆M:x2+y2-2ax-2(8-a)y+4a+22=0,平面内是还有存在定点P,过点P作圆C的一条切线,切点为T1,过点P作圆M的一条切线,切点为T2,使无穷多个圆M,满足$\frac{P{T}_{1}}{P{T}_{2}}$=$\frac{1}{2}$?如果存在,求出所有这样的点P;如果不存在,请说明理由.
设圆C:(x+4)2+y2=16,动圆M:x2+y2-2ax-2(8-a)y+4a+22=0,平面内是还有存在定点P,过点P作圆C的一条切线,切点为T1,过点P作圆M的一条切线,切点为T2,使无穷多个圆M,满足$\frac{P{T}_{1}}{P{T}_{2}}$=$\frac{1}{2}$?如果存在,求出所有这样的点P;如果不存在,请说明理由.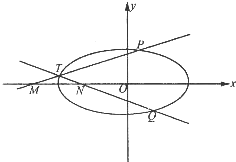 如图所示,椭圆C的离心率为$\frac{\sqrt{3}}{2}$,以坐标原点O为圆心,椭圆C的短半轴长为半径的圆与直线y=$\sqrt{3}$x+2相切.
如图所示,椭圆C的离心率为$\frac{\sqrt{3}}{2}$,以坐标原点O为圆心,椭圆C的短半轴长为半径的圆与直线y=$\sqrt{3}$x+2相切.