题目内容
8.若某几何体的三视图是如图所示的三个直角三角形,则该几何体的外接球的表面积为50π.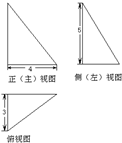
分析 几何体复原为底面是直角三角形,一条侧棱垂直底面直角顶点的三棱锥,扩展为长方体,长方体的对角线的长,就是外接球的直径,然后求其的表面积.
解答 解:由三视图复原几何体,几何体是底面是直角三角形,
一条侧棱垂直底面直角顶点的三棱锥;扩展为长方体,
其外接与球,它的对角线的长为球的直径,
得长方体的体对角线的长为$\sqrt{{3}^{2}+{4}^{2}+{5}^{2}}$=5$\sqrt{2}$,
∴长方体的外接球的半径为$\frac{5\sqrt{2}}{2}$,
∴球的表面积为4π$(\frac{5\sqrt{2}}{2})^{2}$=50π,
故答案为:50π.
点评 本题考查三视图,几何体的外接球的表面积,考查空间想象能力,计算能力,是基础题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
18.已知命题p:“?∈[1,e],a>lnx”,命题q:“?x∈R,x2-4x+a=0””若“p∧q”是真命题,则实数a的取值范围是( )
| A. | (1,4] | B. | (0,1] | C. | [-1,1] | D. | (4,+∞) |
19.某种饮料每箱装6听,如果其中有2听不合格,问质检人员从中随机抽出2听,检测出不合格产品的概率为( )
| A. | $\frac{2}{5}$ | B. | $\frac{8}{15}$ | C. | $\frac{3}{5}$ | D. | $\frac{9}{10}$ |
20.已知函数f(x)=cos2x-$\frac{1}{2}$,则( )
| A. | f(x)为偶函数且最小正周期为π | B. | f(x)为奇函数且最小正周期为π | ||
| C. | f(x)为偶函数且最小正周期为2π | D. | f(x)为奇函数且最小正周期为2π |
17.已知命题p:?x∈R,x-2>0,命题q:?x∈R,2x>x2,则下列说法中正确的是( )
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∧(¬q)是真命题 | D. | 命题p∨(¬q)是假命题 |
18.已知复数z=$\frac{-1-2i}{{{{(1+i)}^2}}}$,则$\overline z$=( )
| A. | -$\frac{3}{4}+\frac{1}{4}$i | B. | -$\frac{1}{4}+\frac{3}{4}$i | C. | -1+$\frac{1}{2}$i | D. | -1-$\frac{1}{2}$i |