题目内容
9.已知函数f(x)=$\left\{{\begin{array}{l}{x+\frac{1}{x},x>0}\\{{x^3}+3,x≤0}\end{array}}$,当2<a≤3时,则方程f(2x2+x)=a的根最多个数是( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
分析 作出函数f(x)的图象,利用换元法令t=2x2+x,利用数形结合进行讨论即可得到结论.
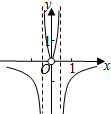
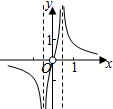
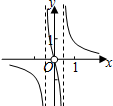
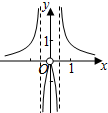
解答 画出函数f(x)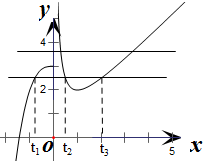 的图象如右图,
的图象如右图,
令t=2x2+x,
当2<a≤3时,y=a与y=f(t)的图象有三个交点,
三个交点的横坐标记为t1,t2,t3且t1≤0<t2<t3,
当2x2+x=t2时,该方程有两解,2x2+x=t3时,
该方程也有两解,2x2+x=t1时,该方程有0个解或1个解或2个解,
∴当2<a≤3时,
方程f(2x2+x)=a的根的个数可能为4个,5个,6个;
当a>3时,y=a与y=f(t)的图象有两个交点,
两个交点的横坐标记为t4,t5且0<t4<t5,
当2x2+x=t4时,该方程有两解,2x2+x=t5时,该方程也有两解,
∴当a>3时,方程f(2x2+x)=a的根的个数为4个;
综上方程f(2x2+x)=a(a>2)的根的个数可能为4个,5个,6个.
即根数最多为6个,
故选:C.
点评 本题主要考查根的个数的判断,利用换元法将方程转化为两个函数的相交问题,以及利用数形结合是解决本题的关键.综合性较强,难度较大.

练习册系列答案
相关题目
19.某种饮料每箱装6听,如果其中有2听不合格,问质检人员从中随机抽出2听,检测出不合格产品的概率为( )
| A. | $\frac{2}{5}$ | B. | $\frac{8}{15}$ | C. | $\frac{3}{5}$ | D. | $\frac{9}{10}$ |
20.已知函数f(x)=cos2x-$\frac{1}{2}$,则( )
| A. | f(x)为偶函数且最小正周期为π | B. | f(x)为奇函数且最小正周期为π | ||
| C. | f(x)为偶函数且最小正周期为2π | D. | f(x)为奇函数且最小正周期为2π |
17.已知命题p:?x∈R,x-2>0,命题q:?x∈R,2x>x2,则下列说法中正确的是( )
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∧(¬q)是真命题 | D. | 命题p∨(¬q)是假命题 |
4.设点P为双曲线C1:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)和圆C2:x2+y2=a2+b2的一个交点,F1,F2为双曲线C1的左、右焦点.若2∠PF1F2=∠PF2F1,则双曲线C1的离心率为( )
| A. | $\sqrt{3}$+1 | B. | $\sqrt{2}$+1 | C. | $\sqrt{3}$ | D. | 2 |
18.已知复数z=$\frac{-1-2i}{{{{(1+i)}^2}}}$,则$\overline z$=( )
| A. | -$\frac{3}{4}+\frac{1}{4}$i | B. | -$\frac{1}{4}+\frac{3}{4}$i | C. | -1+$\frac{1}{2}$i | D. | -1-$\frac{1}{2}$i |
19.已知命题p:?x∈R,ex>0命题q:?x∈R,x-2>x2,则( )
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∧(?q)是真命题 | D. | 命题p∨(?q)是假命题 |