题目内容
1.设x,y∈R,向量$\overrightarrow{a}$=(x,1),$\overrightarrow{b}$=(1,y),$\overrightarrow{c}$=(2,-4)且$\overrightarrow{a}$⊥$\overrightarrow{c}$,$\overrightarrow{b}$∥$\overrightarrow{c}$,则|$\overrightarrow{a}$+$\overrightarrow{b}$|=( )| A. | 2$\sqrt{5}$ | B. | $\sqrt{10}$ | C. | 3$\sqrt{5}$ | D. | $\sqrt{5}$ |
分析 由$\overrightarrow{a}⊥\overrightarrow{b}$,便有$\overrightarrow{a}•\overrightarrow{b}=0$,这样可以求出x,而由$\overrightarrow{b}$∥$\overrightarrow{c}$,便有-4-2y=0,这样可求出y,从而得出向量$\overrightarrow{a}+\overrightarrow{b}$的坐标,根据坐标即可得出其长度.
解答 解:$\overrightarrow{a}⊥\overrightarrow{c}$;
∴$\overrightarrow{a}•\overrightarrow{c}=2x-4=0$;
∴x=2;
$\overrightarrow{b}$∥$\overrightarrow{c}$;
∴1•(-4)-y•2=0;
∴y=-2;
∴$\overrightarrow{a}+\overrightarrow{b}=(3,-1)$;
∴$|\overrightarrow{a}+\overrightarrow{b}|=\sqrt{10}$.
故选:B.
点评 考查非零向量垂直的充要条件,数量积、向量加法的坐标运算,以及平行向量的坐标关系,根据向量坐标求向量长度.

练习册系列答案
相关题目
9.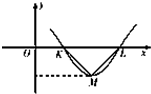 设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,$\overrightarrow{MK}•\overrightarrow{ML}$=0,|KL|=1,|ML|=$\frac{{\sqrt{2}}}{2}$,则$f(\frac{1}{6})$的值为( )
设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,$\overrightarrow{MK}•\overrightarrow{ML}$=0,|KL|=1,|ML|=$\frac{{\sqrt{2}}}{2}$,则$f(\frac{1}{6})$的值为( )
 设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,$\overrightarrow{MK}•\overrightarrow{ML}$=0,|KL|=1,|ML|=$\frac{{\sqrt{2}}}{2}$,则$f(\frac{1}{6})$的值为( )
设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,$\overrightarrow{MK}•\overrightarrow{ML}$=0,|KL|=1,|ML|=$\frac{{\sqrt{2}}}{2}$,则$f(\frac{1}{6})$的值为( )| A. | $-\frac{{\sqrt{3}}}{4}$ | B. | $-\frac{1}{4}$ | C. | $-\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
16.若函数f(x)=$\left\{\begin{array}{l}{{x}^{3}-2x+{a}^{2},x≤1}\\{\frac{15a}{3x+1},x>1}\end{array}\right.$在点x=1处连续,则实数a等于( )
| A. | 4 | B. | -$\frac{1}{4}$ | C. | -$\frac{1}{4}$或-4 | D. | -$\frac{1}{4}$或4 |
13.P为抛物线x2=-4y上一点,A(1,0),则点P到此抛物线的准线的距离与P到点A的距离之和的最小值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{2}$ |
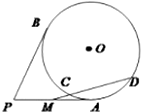 如图,P是圆O外一点,PA、PB是圆O的两条切线,切点分别为A、B,PA的中点为M,过M作圆O的一条割线交圆O于C、D两点,若PB=2$\sqrt{3}$,MC=1,则CD=2.
如图,P是圆O外一点,PA、PB是圆O的两条切线,切点分别为A、B,PA的中点为M,过M作圆O的一条割线交圆O于C、D两点,若PB=2$\sqrt{3}$,MC=1,则CD=2.