题目内容
11．求证：两条直线相交，只有一个交点．分析 用反证法进行证明；先假设原命题不成立，然后经过推导得出与已知或定理相矛盾，从而证得原结论正确．
解答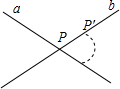 
解：已知直线a，b，求证：直线a，b相交时只有一个交点P．
证明：假设a，b相交时不止一个交点P，不妨设其他交点中有一个为P′，
则点P和点P′在直线a上又在直线b上，
那么经过P和P′的直线就有两条，
这与“两点决定一条直线”相矛盾，
因此假设不成立，
所以两条直线相交只有一个交点．
点评 解此题关键要懂得反证法的意义及步骤．反证法的步骤是：
（1）假设结论不成立；
（2）从假设出发推出矛盾；
（3）假设不成立，则结论成立．
在假设结论不成立时要注意考虑结论的反面所有可能的情况，如果只有一种，那么否定一种就可以了，如果有多种情况，只要否定其一即可．
练习册系列答案
相关题目
1．设x，y∈R，向量$\overrightarrow{a}$=（x，1），$\overrightarrow{b}$=（1，y），$\overrightarrow{c}$=（2，-4）且$\overrightarrow{a}$⊥$\overrightarrow{c}$，$\overrightarrow{b}$∥$\overrightarrow{c}$，则|$\overrightarrow{a}$+$\overrightarrow{b}$|=（ ）
| A． | 2$\sqrt{5}$ | B． | $\sqrt{10}$ | C． | 3$\sqrt{5}$ | D． | $\sqrt{5}$ |
2．不等式3x2-2x-1＜0的解集是（ ）
| A． | $（{-\frac{1}{3}，1}）$ | B． | （1，+∞） | C． | $（{-∞，-\frac{1}{3}}）∪（{1，+∞}）$ | D． | $（{-∞，-\frac{1}{3}}）$ |
19．过抛物线y2=4x焦点F的直线l交抛物线于点A，B两点，且AF=2BF，则直线l的斜率为（ ）
| A． | $\sqrt{2}$ | B． | $±2\sqrt{2}$ | C． | $±\sqrt{2}$ | D． | 2$\sqrt{2}$ |