题目内容
9.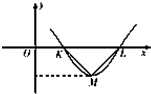 设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,$\overrightarrow{MK}•\overrightarrow{ML}$=0,|KL|=1,|ML|=$\frac{{\sqrt{2}}}{2}$,则$f(\frac{1}{6})$的值为( )
设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,$\overrightarrow{MK}•\overrightarrow{ML}$=0,|KL|=1,|ML|=$\frac{{\sqrt{2}}}{2}$,则$f(\frac{1}{6})$的值为( )| A. | $-\frac{{\sqrt{3}}}{4}$ | B. | $-\frac{1}{4}$ | C. | $-\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
分析 利用函数的图象,通过KL=1以及∠KML=90°求出求出A,再求出函数的周期,确定ω,利用函数是偶函数求出φ,得到函数的解析式,即可求解f($\frac{1}{6}$)的值.
解答 解:因为f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,
$\overrightarrow{MK}•\overrightarrow{ML}$=0,∠KML=90°,|KL|=1,|ML|=$\frac{{\sqrt{2}}}{2}$,可得|KM|=$\frac{{\sqrt{2}}}{2}$,
所以解得:A=$\frac{1}{2}$,T=2,因为T=$\frac{2π}{ω}$,所以ω=π,
函数是偶函数,0<φ<π,所以φ=$\frac{π}{2}$,
∴函数的解析式为:f(x)=$\frac{1}{2}$sin(πx+$\frac{π}{2}$),
所以f($\frac{1}{6}$)=$\frac{1}{2}$sin($\frac{π}{6}$+$\frac{π}{2}$)=$\frac{1}{2}$cos$\frac{π}{6}$=$\frac{\sqrt{3}}{4}$.
故选:D.
点评 本题考查函数的解析式的求法,函数奇偶性的应用,考查学生识图能力、计算能力,属于基本知识的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.设x,y∈R,向量$\overrightarrow{a}$=(x,1),$\overrightarrow{b}$=(1,y),$\overrightarrow{c}$=(2,-4)且$\overrightarrow{a}$⊥$\overrightarrow{c}$,$\overrightarrow{b}$∥$\overrightarrow{c}$,则|$\overrightarrow{a}$+$\overrightarrow{b}$|=( )
| A. | 2$\sqrt{5}$ | B. | $\sqrt{10}$ | C. | 3$\sqrt{5}$ | D. | $\sqrt{5}$ |
19.过抛物线y2=4x焦点F的直线l交抛物线于点A,B两点,且AF=2BF,则直线l的斜率为( )
| A. | $\sqrt{2}$ | B. | $±2\sqrt{2}$ | C. | $±\sqrt{2}$ | D. | 2$\sqrt{2}$ |


 △ABC中,AD是BC边上中线,E为AD上一点,BE的延长线交AC于F,交AB的平行线CG于G.
△ABC中,AD是BC边上中线,E为AD上一点,BE的延长线交AC于F,交AB的平行线CG于G.