题目内容
M是抛物线y2=4x上的一点,F是抛物线的焦点,以Fx为始边,FM为终边的∠xFM=60°,则|FM|=______.
由题意,得F(1,0)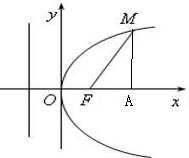
设M(m,n),过点M作MA垂直于x轴,垂足为A
∵Rt△AFM中,∠AFM=60°,
∴|MF|=2|FA|即|FM|=2(m-1),|MF|=
∵|MA|=|n|,∴即|MF|=
所以2(m-1)=
,整理得n2=3(m-1)2…①
又∵M是抛物线y2=4x上一点,∴n2=4m…②
联解①②,得m=3或m=
(小于1舍去)
∴|FM|=2(m-1)=4
故答案为:4

设M(m,n),过点M作MA垂直于x轴,垂足为A
∵Rt△AFM中,∠AFM=60°,
∴|MF|=2|FA|即|FM|=2(m-1),|MF|=
| 2|MA| | ||
|
∵|MA|=|n|,∴即|MF|=
| 2|n| | ||
|
所以2(m-1)=
| 2|n| | ||
|
又∵M是抛物线y2=4x上一点,∴n2=4m…②
联解①②,得m=3或m=
| 1 |
| 3 |
∴|FM|=2(m-1)=4
故答案为:4

练习册系列答案
相关题目