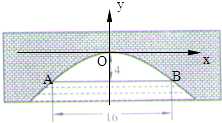
题目内容
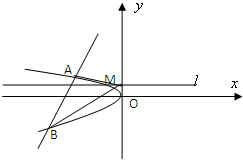
过抛物线y2=2x内的任意一点Q(s,t)(t2<2s)作两条相互垂直的弦AB,CD,若弦AB,CD的中点分别为M,N,直线MN恒过定点( )
| A.(s+1,0) | B.(|1-s|,0) | C.(1+2s,0) | D.(|1-2s|,0) |
不妨取Q点是抛物线的焦点(
,0).
设点A(x1,y1),B(x2,y2),M(x3,y3),N(x4,y4)
把直线AB:y=k(x-
)代入y2=2x,得
k2x2-(k2+2)x+
k2=0,
∴x3=
=
+
,y3=k(x3-
)=
同理可得,x4=
+k2,y4=-k,
∴kMN=
=
∴直线MN为y-
=
(x-
-
),即y=
(x-
),
结合直线方程的点斜式,可得直线恒过定点P(
,0),
对照Q点是抛物线的焦点(
,0),定点P可以写成(
+1,0).
故选A.
| 1 |
| 2 |
设点A(x1,y1),B(x2,y2),M(x3,y3),N(x4,y4)
把直线AB:y=k(x-
| 1 |
| 2 |
k2x2-(k2+2)x+
| 1 |
| 4 |
∴x3=
| x1+x2 |
| 2 |
| 1 |
| 2 |
| 1 |
| k2 |
| 1 |
| 2 |
| 1 |
| k |
同理可得,x4=
| 1 |
| 2 |
∴kMN=
| y3-y4 |
| x3-x4 |
| k |
| 1-k2 |
∴直线MN为y-
| 1 |
| k |
| k |
| 1-k2 |
| 1 |
| 2 |
| 1 |
| k2 |
| k |
| 1-k2 |
| 3 |
| 2 |
结合直线方程的点斜式,可得直线恒过定点P(
| 3 |
| 2 |
对照Q点是抛物线的焦点(
| 1 |
| 2 |
| 1 |
| 2 |
故选A.

练习册系列答案
相关题目
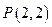 为
为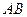 的中点,则抛物线C的方程为 .
的中点,则抛物线C的方程为 .