题目内容
抛物线y2=4x的焦点为F,A(x1,y1),B(x2,y2),(x1>x2,y1>0,y2<0)在抛物线上且A,B,F三点共线且|AB|=
求(1)直线AB的方程.
(2)△AOB外接圆方程.
| 25 |
| 4 |
求(1)直线AB的方程.
(2)△AOB外接圆方程.
(1)∵y2=4x的焦点F(1,0),
依题意,设直线AB的方程为y=k(x-1),因为|AB|=
,
由抛物线的定义可得:|AB|=|AA′|+|BB′|=x1+1+x2+1=
,
∴x1+x2=
.
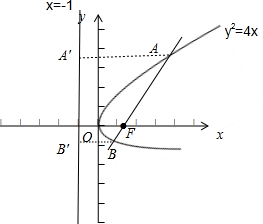
由
得:k2x2-(2k2+4)x+k2=0,
∴x1+x2=
=
,
∴k2=
,又k>0,
∴k=
.
∴直线AB的方程为:y=
(x-1).
(2)将k2=
代入k2x2-(2k2+4)x+k2=0得:4x2-17x+4=0,
∴x=
或x=4,即x1=4,x2=
,将x1,x2分别代入直线AB的方程y=
(x-1)得:y1=4,y2=-1.
∴A(4,4),B(
,-1).
设△AOB外接圆方程为x2+y2+Dx+Ey+F=0,
则:
,解得
.
故△AOB外接圆方程为x2+y2-
x-
y=0.
依题意,设直线AB的方程为y=k(x-1),因为|AB|=
| 25 |
| 4 |
由抛物线的定义可得:|AB|=|AA′|+|BB′|=x1+1+x2+1=
| 25 |
| 4 |
∴x1+x2=
| 17 |
| 4 |
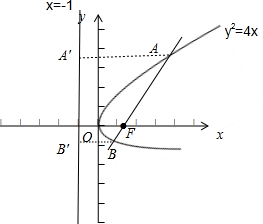
由
|
∴x1+x2=
| 2k2+4 |
| k2 |
| 17 |
| 4 |
∴k2=
| 16 |
| 9 |
∴k=
| 4 |
| 3 |
∴直线AB的方程为:y=
| 4 |
| 3 |
(2)将k2=
| 16 |
| 9 |
∴x=
| 1 |
| 4 |
| 1 |
| 4 |
| 4 |
| 3 |
∴A(4,4),B(
| 1 |
| 4 |
设△AOB外接圆方程为x2+y2+Dx+Ey+F=0,
则:
|
|
故△AOB外接圆方程为x2+y2-
| 29 |
| 4 |
| 3 |
| 4 |

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目