题目内容
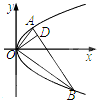
如图,点A,B在抛物线y2=2px(p>0)上,且OA⊥OB,OD⊥AB交AB于D,则点D在( )
| A.某个圆上运动 | B.某个椭圆上运动 |
| C.某个双曲线上运动 | D.某个抛物线上运动 |

设A(x1,y1),B(x2,y2),D(x,y),(y1≠y2)则
∵OA⊥OB,∴x1x2+y1y2=0
∵点A,B在抛物线y2=2px
∴y12y22=4p2x1x2,
∴y1y2=-4p2,
∵OD⊥AB,∴
•
=-1
∴
•
=-1
∵A,D,B共线,
=(x-x1,y-y1),
=(x-x2,y-y2)
∴(x-x1)(y-y2)=(y-y1)(x-x2)
∴x•(y1-y2)+y•
+
=0
∴x-y•
-2p=0
∴x-y•(-
)-2p=0
∴x2+y2-2px=0,(x≠0).
即D点的轨迹方程为x2+y2-2px=0,(x≠0).
故选D.
∵OA⊥OB,∴x1x2+y1y2=0
∵点A,B在抛物线y2=2px
∴y12y22=4p2x1x2,
∴y1y2=-4p2,
∵OD⊥AB,∴
| y |
| x |
| y2-y1 |
| x2-x1 |
∴
| y |
| x |
| 2p |
| y2+y1 |
∵A,D,B共线,
| AD |
| BD |
∴(x-x1)(y-y2)=(y-y1)(x-x2)
∴x•(y1-y2)+y•
| y22-y12 |
| 2p |
| y1y2(y1-y2) |
| 2p |
∴x-y•
| y1+y2 |
| 2p |
∴x-y•(-
| y |
| x |
∴x2+y2-2px=0,(x≠0).
即D点的轨迹方程为x2+y2-2px=0,(x≠0).
故选D.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目