题目内容
20.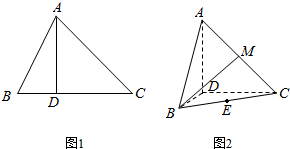 已知△ABC中,∠ACB=45°,B、C为定点且BC=3,A为动点,作AD⊥BC于D(异于点B),如图1所示.连接AB,将△ABD沿AD折起,使平面ABD⊥平面ADC,如图2所示.
已知△ABC中,∠ACB=45°,B、C为定点且BC=3,A为动点,作AD⊥BC于D(异于点B),如图1所示.连接AB,将△ABD沿AD折起,使平面ABD⊥平面ADC,如图2所示.(Ⅰ)求证:AB⊥CD;
(Ⅱ)当三棱锥A-BCD的体积取得最大值时,求线段AC的长;
(Ⅲ)在(Ⅱ)的条件下,分别取BC,AC的中点E、M,试在棱CD上确定一点N,使得EN⊥BM,并求此时EN与平面BMN所成角的大小.
分析 (Ⅰ)证明CD⊥平面ABD,即可证明AB⊥CD;
(Ⅱ)设BD=x,先利用线面垂直的判定定理证明AD即为三棱锥A-BCD的高,再将三棱锥的体积表示为x的函数,最后利用导数求函数的最大值即可;
(Ⅲ)由(Ⅱ)可先建立空间直角坐标系,写出相关点的坐标和相关向量的坐标,设出动点N的坐标,先利用线线垂直的充要条件计算出N点坐标,从而确定N点位置,再求平面BMN的法向量,从而利用夹角公式即可求得所求线面角
解答  (Ⅰ)证明:∵BD⊥AD,CD⊥AD,平面ABD⊥平面ADC,
(Ⅰ)证明:∵BD⊥AD,CD⊥AD,平面ABD⊥平面ADC,
∴∠BDC=90°,
∴CD⊥BD,
∵CD⊥AD,AD∩BD=D,
∴CD⊥平面ABD,
∵AB?平面ABD,
∴AB⊥CD;
(Ⅱ)解:设BD=x,则CD=3-x
∵∠ACB=45°,AD⊥BC,∴AD=CD=3-x
∵折起前AD⊥BC,∴折起后AD⊥BD,AD⊥CD,BD∩DC=D
∴AD⊥平面BCD
∴VA-BCD=$\frac{1}{3}$×AD×S△BCD=$\frac{1}{3}$×(3-x)×$\frac{1}{2}$×x(3-x)=$\frac{1}{6}$(x3-6x2+9x)
设f(x)=$\frac{1}{6}$(x3-6x2+9x) x∈(0,3),
∵f′(x)=$\frac{1}{2}$(x-1)(x-3),∴f(x)在(0,1)上为增函数,在(1,3)上为减函数
∴当x=1时,函数f(x)取最大值
∴当BD=1时,三棱锥A-BCD的体积最大,此时AC=2$\sqrt{2}$;
(Ⅲ)解:以D为原点,建立如图直角坐标系D-xyz,由(Ⅱ)知,三棱锥A-BCD的体积最大时,BD=1,AD=CD=2
∴D(0,0,0),B(1,0,0),C(0,2,0),A(0,0,2),M(0,1,1),E($\frac{1}{2}$,1,0),
且$\overrightarrow{BM}$=(-1,1,1)
设N(0,λ,0),则$\overrightarrow{EN}$=(-$\frac{1}{2}$,λ-1,0)
∵EN⊥BM,∴$\overrightarrow{EN}$•$\overrightarrow{BM}$=0
即(-1,1,1)•(-$\frac{1}{2}$,λ-1,0)=$\frac{1}{2}$+λ-1=0,∴λ=$\frac{1}{2}$,∴N(0,$\frac{1}{2}$,0)
∴当DN=$\frac{1}{2}$时,EN⊥BM
设平面BMN的一个法向量为$\overrightarrow{n}$=(x,y,z),
由$\overrightarrow{BM}$=(-1,1,1)及$\overrightarrow{BN}$=(-1,$\frac{1}{2}$,0)
得$\left\{\begin{array}{l}{y=2x}\\{z=-x}\end{array}\right.$,取$\overrightarrow{n}$=(1,2,-1)
设EN与平面BMN所成角为θ,则$\overrightarrow{EN}$=(-$\frac{1}{2}$,-$\frac{1}{2}$,0)
sinθ=|cos<$\overrightarrow{EN}$,$\overrightarrow{n}$>|=$\frac{|-\frac{1}{2}-1|}{\sqrt{6}×\frac{\sqrt{2}}{2}}$=$\frac{\sqrt{3}}{2}$
∴θ=60°
∴EN与平面BMN所成角的大小为60°.
点评 本题主要考查了线面垂直的判定,折叠问题中的不变量,空间线面角的计算方法,空间向量、空间直角坐标系的运用,有一定的运算量,属中档题.

| A. | (-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$) | B. | (-∞,-$\frac{\sqrt{3}}{3}$)∪($\frac{\sqrt{3}}{3}$,+∞) | C. | [-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$] | D. | (-$\frac{\sqrt{3}}{3}$,0)∪(0,$\frac{\sqrt{3}}{3}$) |
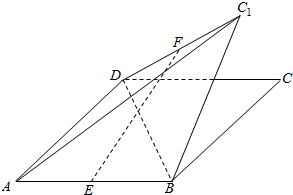 如图,四边形ABCD为平行四边形,AB=5,AD=4,BD=3,将△BCD沿着BD翻折到平面BC1D处,E,F分别为边AB,C1D的中点.
如图,四边形ABCD为平行四边形,AB=5,AD=4,BD=3,将△BCD沿着BD翻折到平面BC1D处,E,F分别为边AB,C1D的中点.