题目内容
9.求值:tan250°•sin80°•($\sqrt{3}$tan20°-1).分析 由条件利用诱导公式、辅助角公式、二倍角公式求得所给式子的值.
解答 解:tan250°•sin80°•($\sqrt{3}$tan20°-1)=tan70°•cos10°•$\frac{\sqrt{3}sin20°-cos20°}{cos20°}$
=tan70°•cos10°•$\frac{2sin(20°-30°)}{cos20°}$=tan70°•cos10°•$\frac{-2sin10°}{cos20°}$
=cot20°•(-tan20°)=-1.
点评 本题主要考查诱导公式、辅助角公式、二倍角公式的应用,属于基础题.

练习册系列答案
相关题目
19.若函数f(x)=$\left\{\begin{array}{l}{x^2}-5x,x≥0\\-{x^2}+ax,x<0\end{array}$是奇函数,则实数a的值是( )
| A. | -10 | B. | 10 | C. | -5 | D. | 5 |
17.若sinxcosy+cosxsiny=$\frac{1}{2}$,cos2x-cos2y=$\frac{2}{3}$,则sin(x-y)等于( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
5.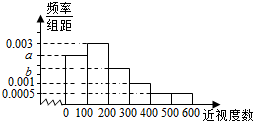 某普通高中为了了解学生的视力状况,随机抽查了100名高二年级学生和100名高三年级学生,对这些学生配戴眼镜的度数(简称:近视度数)进行统计,得到高二学生的频数分布表和高三学生频率分布直方图如下:
某普通高中为了了解学生的视力状况,随机抽查了100名高二年级学生和100名高三年级学生,对这些学生配戴眼镜的度数(简称:近视度数)进行统计,得到高二学生的频数分布表和高三学生频率分布直方图如下:
将近视程度由低到高分为4个等级:当近视度数在0-100时,称为不近视,记作0;当近视度数在100-200时,称为轻度近视,记作1;当近视度数在200-400时,称为中度近视,记作2;当近视度数在400以上时,称为高度近视,记作3.
(Ⅰ)从该校任选1名高二学生,估计该生近视程度未达到中度及以上的概率;
(Ⅱ)设a=0.0024,从该校任选1名高三学生,估计该生近视程度达到中度或中度以上的概率;
(Ⅲ)把频率近似地看成概率,用随机变量X,Y分别表示高二、高三年级学生的近视程度,若EX=EY,求b.
 某普通高中为了了解学生的视力状况,随机抽查了100名高二年级学生和100名高三年级学生,对这些学生配戴眼镜的度数(简称:近视度数)进行统计,得到高二学生的频数分布表和高三学生频率分布直方图如下:
某普通高中为了了解学生的视力状况,随机抽查了100名高二年级学生和100名高三年级学生,对这些学生配戴眼镜的度数(简称:近视度数)进行统计,得到高二学生的频数分布表和高三学生频率分布直方图如下:| 近视度数 | 0-100 | 100-200 | 200-300 | 300-400 | 400以上 |
| 学生频数 | 30 | 40 | 20 | 10 | 0 |
(Ⅰ)从该校任选1名高二学生,估计该生近视程度未达到中度及以上的概率;
(Ⅱ)设a=0.0024,从该校任选1名高三学生,估计该生近视程度达到中度或中度以上的概率;
(Ⅲ)把频率近似地看成概率,用随机变量X,Y分别表示高二、高三年级学生的近视程度,若EX=EY,求b.
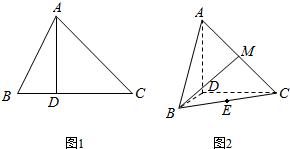 已知△ABC中,∠ACB=45°,B、C为定点且BC=3,A为动点,作AD⊥BC于D(异于点B),如图1所示.连接AB,将△ABD沿AD折起,使平面ABD⊥平面ADC,如图2所示.
已知△ABC中,∠ACB=45°,B、C为定点且BC=3,A为动点,作AD⊥BC于D(异于点B),如图1所示.连接AB,将△ABD沿AD折起,使平面ABD⊥平面ADC,如图2所示.