题目内容
12. 如图,四边形ABCD为平行四边形,AB=5,AD=4,BD=3,将△BCD沿着BD翻折到平面BC1D处,E,F分别为边AB,C1D的中点.
如图,四边形ABCD为平行四边形,AB=5,AD=4,BD=3,将△BCD沿着BD翻折到平面BC1D处,E,F分别为边AB,C1D的中点.(Ⅰ)求证:EF∥平面BCC1;
(Ⅱ)若异面直线EF,BC1所成的角为30°,求直线C1D与平面ABCD所成角的正弦值.
分析 (Ⅰ)先连接CC1,取CC1的中点G,并连接FG,BG,从而可说明四边形FGBE为平行四边形,从而得到EF∥BG,根据线面平行的判定定理即可得到EF∥平面BCC1;
(Ⅱ)容易说明∠C1BG=30°,从而得到∠C1BC=60°,从而△BCC1为等边三角形,能够说明直线AB⊥平面BCC1,从而得到平面ABCD⊥平面BCC1.取BC中点H,连接C1H,从而有C1H⊥BC,根据面面垂直的性质定理即知C1H⊥平面ABCD,连接DH,∠C1DH便是直线C1D和平面ABCD所成的角,根据已知边的长度即可求C1D,C1H,从而能求出sin∠C1DH.
解答 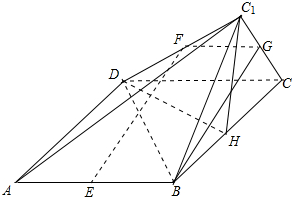 解:(Ⅰ)证明:连接CC1,取CC1的中点G,连接FG,BG,则:
解:(Ⅰ)证明:连接CC1,取CC1的中点G,连接FG,BG,则:
∵四边形ABCD是平行四边形,E,F分别为AB,C1D的中点;
∴FG∥BE,且FG=BE;
∴四边形BEFG是平行四边形;
∴EF∥BG,BG?平面BCC1,EF?平面BCC1;
∴EF∥平面BCC1;
(Ⅱ)由(Ⅰ)可知,∠C1BG为异面直线EF,BC1所成的角,∴∠C1BG=30°,∠C1BC=60°;
又BC=BC1,∴△C1BC为等边三角形;
AB=5,AD=4,BD=3,∴∠ADB=∠CBD=∠C1BD=90°;
∴BD⊥BC,BD⊥BC1,且BC∩BC1=B;
∴BD⊥平面BCC1;
∴平面ABCD⊥平面BCC1,平面ABCD∩平面BCC1=BC;
取BC中点H,连接C1H,则C1H⊥平面ABCD;
连接DH,则∠C1DH即为直线C1D和平面ABCD所成的角;
∴$sin∠{C}_{1}DH=\frac{{C}_{1}H}{{C}_{1}D}=\frac{2\sqrt{3}}{5}$;
∴直线C1D与平面ABCD所成角的正弦值为$\frac{2\sqrt{3}}{5}$.
点评 考查三角形中位线的性质,平行四边形的定义,线面平行的判定定理,异面直线所成角的定义,线面垂直、面面垂直的判定定理,以及面面垂直的性质定理,线面角的定义及求法.

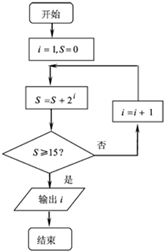
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
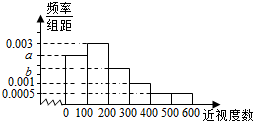 某普通高中为了了解学生的视力状况,随机抽查了100名高二年级学生和100名高三年级学生,对这些学生配戴眼镜的度数(简称:近视度数)进行统计,得到高二学生的频数分布表和高三学生频率分布直方图如下:
某普通高中为了了解学生的视力状况,随机抽查了100名高二年级学生和100名高三年级学生,对这些学生配戴眼镜的度数(简称:近视度数)进行统计,得到高二学生的频数分布表和高三学生频率分布直方图如下:| 近视度数 | 0-100 | 100-200 | 200-300 | 300-400 | 400以上 |
| 学生频数 | 30 | 40 | 20 | 10 | 0 |
(Ⅰ)从该校任选1名高二学生,估计该生近视程度未达到中度及以上的概率;
(Ⅱ)设a=0.0024,从该校任选1名高三学生,估计该生近视程度达到中度或中度以上的概率;
(Ⅲ)把频率近似地看成概率,用随机变量X,Y分别表示高二、高三年级学生的近视程度,若EX=EY,求b.
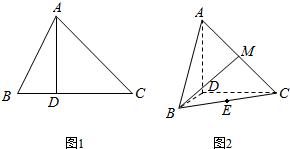 已知△ABC中,∠ACB=45°,B、C为定点且BC=3,A为动点,作AD⊥BC于D(异于点B),如图1所示.连接AB,将△ABD沿AD折起,使平面ABD⊥平面ADC,如图2所示.
已知△ABC中,∠ACB=45°,B、C为定点且BC=3,A为动点,作AD⊥BC于D(异于点B),如图1所示.连接AB,将△ABD沿AD折起,使平面ABD⊥平面ADC,如图2所示.