题目内容
14.如图,设钝角α的顶点位于坐标原点O,始边与x轴的非负半轴重合,终边与单位圆O相交于点P,且点P的坐标为(-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$).
(1)写出sinα和cosα的值;
(2)求sin(2α+$\frac{π}{6}$)的值.
分析 (1)直接利用三角函数的定义,写出结果即可.
(2)利用两角和与差的三角函数,化简求解即可.
解答 解:(1)由任意角的三角函数的定义可知:sinα=$\frac{1}{2}$,cosα=$-\frac{\sqrt{3}}{2}$.
(2)sin(2α+$\frac{π}{6}$)=sin2αcos$\frac{π}{6}$+sin$\frac{π}{6}$cos2α=2×$\frac{1}{2}×(-\frac{\sqrt{3}}{2})×\frac{\sqrt{3}}{2}$+$\frac{1}{2}×(1-2×({\frac{1}{2})}^{2})$=$-\frac{3}{4}+\frac{1}{4}$
=$-\frac{1}{2}$.
点评 本题考查任意角的三角函数的定义,两角和与差的三角函数以及二倍角公式的应用,考查计算能力.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
5.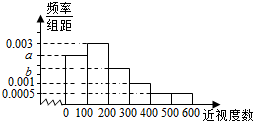 某普通高中为了了解学生的视力状况,随机抽查了100名高二年级学生和100名高三年级学生,对这些学生配戴眼镜的度数(简称:近视度数)进行统计,得到高二学生的频数分布表和高三学生频率分布直方图如下:
某普通高中为了了解学生的视力状况,随机抽查了100名高二年级学生和100名高三年级学生,对这些学生配戴眼镜的度数(简称:近视度数)进行统计,得到高二学生的频数分布表和高三学生频率分布直方图如下:
将近视程度由低到高分为4个等级:当近视度数在0-100时,称为不近视,记作0;当近视度数在100-200时,称为轻度近视,记作1;当近视度数在200-400时,称为中度近视,记作2;当近视度数在400以上时,称为高度近视,记作3.
(Ⅰ)从该校任选1名高二学生,估计该生近视程度未达到中度及以上的概率;
(Ⅱ)设a=0.0024,从该校任选1名高三学生,估计该生近视程度达到中度或中度以上的概率;
(Ⅲ)把频率近似地看成概率,用随机变量X,Y分别表示高二、高三年级学生的近视程度,若EX=EY,求b.
 某普通高中为了了解学生的视力状况,随机抽查了100名高二年级学生和100名高三年级学生,对这些学生配戴眼镜的度数(简称:近视度数)进行统计,得到高二学生的频数分布表和高三学生频率分布直方图如下:
某普通高中为了了解学生的视力状况,随机抽查了100名高二年级学生和100名高三年级学生,对这些学生配戴眼镜的度数(简称:近视度数)进行统计,得到高二学生的频数分布表和高三学生频率分布直方图如下:| 近视度数 | 0-100 | 100-200 | 200-300 | 300-400 | 400以上 |
| 学生频数 | 30 | 40 | 20 | 10 | 0 |
(Ⅰ)从该校任选1名高二学生,估计该生近视程度未达到中度及以上的概率;
(Ⅱ)设a=0.0024,从该校任选1名高三学生,估计该生近视程度达到中度或中度以上的概率;
(Ⅲ)把频率近似地看成概率,用随机变量X,Y分别表示高二、高三年级学生的近视程度,若EX=EY,求b.
9.已知集合A={x|$\frac{2x-2}{x-2}$<1},集合B={x|x2+4x-5>0},集合C={x||x-m|<1,m∈R},求:
(1)A∩B.
(2)若(A∩B)⊆C,求m的取值范围.
(1)A∩B.
(2)若(A∩B)⊆C,求m的取值范围.
19.已知等比数列{an}的首项a1=1,公比q=2,等差数列{bn}的首项b1=3,公差d=3,在{an}中插入{bn}中的项后从小到大构成新数列{cn},则{cn}的第100项为( )
| A. | 270 | B. | 273 | C. | 276 | D. | 279 |
4.设f(x)=(1+x)6(1-x)5,则导函数f′(x)中x2的系数是( )
| A. | 0 | B. | 15 | C. | 12 | D. | -15 |
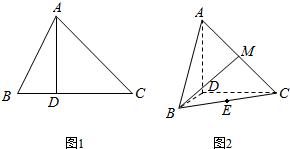 已知△ABC中,∠ACB=45°,B、C为定点且BC=3,A为动点,作AD⊥BC于D(异于点B),如图1所示.连接AB,将△ABD沿AD折起,使平面ABD⊥平面ADC,如图2所示.
已知△ABC中,∠ACB=45°,B、C为定点且BC=3,A为动点,作AD⊥BC于D(异于点B),如图1所示.连接AB,将△ABD沿AD折起,使平面ABD⊥平面ADC,如图2所示.