题目内容
8.某车间分批生产某种产品,每批的生产准备费用为400元.若每批生产x件,则平均仓储时间为$\frac{x}{4}$天,且每件产品每天的仓储费用为1元.为使平均到每件产品的生产准备费用与仓储费用之和最小,每批应生产产品( )| A. | 20件 | B. | 30件 | C. | 40件 | D. | 50 件 |
分析 设平均每件产品的生产准备费用与仓储费用之和为y,推出y的表达式,整理后利用基本不等式可求最小值及相应的x
解答 解:设平均每件产品的生产准备费用与仓储费用之和为y,
则y=$\frac{\frac{x}{4}•x•1+400}{x}$=$\frac{x}{4}+\frac{400}{x}$≥20,
当且仅当$\frac{x}{4}=\frac{400}{x}$,即x=40时“=”成立,
故每批应生产产品40件,
故选:C.
点评 本题主要考查函数与方程的应用,基本不等式在求解实际问题中的最值中的应用,解题的关键是把实际问题转化为数学问题.

练习册系列答案
相关题目
19.若函数f(x)=$\left\{\begin{array}{l}{x^2}-5x,x≥0\\-{x^2}+ax,x<0\end{array}$是奇函数,则实数a的值是( )
| A. | -10 | B. | 10 | C. | -5 | D. | 5 |
13.函数f(x)=Asin(ωx+θ)(A>0,ω>0)的部分图象如图所示,则f($\frac{π}{3}$)的值为( )

| A. | $\sqrt{2}$ | B. | 0 | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
17.若sinxcosy+cosxsiny=$\frac{1}{2}$,cos2x-cos2y=$\frac{2}{3}$,则sin(x-y)等于( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
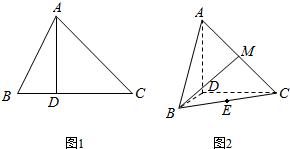 已知△ABC中,∠ACB=45°,B、C为定点且BC=3,A为动点,作AD⊥BC于D(异于点B),如图1所示.连接AB,将△ABD沿AD折起,使平面ABD⊥平面ADC,如图2所示.
已知△ABC中,∠ACB=45°,B、C为定点且BC=3,A为动点,作AD⊥BC于D(异于点B),如图1所示.连接AB,将△ABD沿AD折起,使平面ABD⊥平面ADC,如图2所示.