题目内容
15.若双曲线 C:2x2-y2=m(m>0)与抛物线y2=16x的准线交于A,B两点,且|AB|=4$\sqrt{3}$则m的值是20.分析 求出y2=16x的准线l:x=-4,由C与抛物线y2=16x的准线交于A,B两点,且|AB|=4$\sqrt{3}$,即可求出m的值.
解答 解:y2=16x的准线l:x=-4,
∵C与抛物线y2=16x的准线l:x=-4交于A,B两点,|AB|=4$\sqrt{3}$,
∴A(-4,2$\sqrt{3}$),B(-4,-2$\sqrt{3}$),
将A点坐标代入双曲线方程得2(-4)2-(2$\sqrt{3}$)2=m,
∴m=20,
故答案为:20.
点评 本题考查双曲线的性质和应用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
6.某几何体三视图如下,图中三个等腰三角形的直角边长都是2,该几何体的体积为( )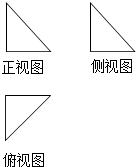

| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 4 | D. | $\frac{16}{3}$ |
7.执行如图所示的程序框图,则输出的i的值是( )
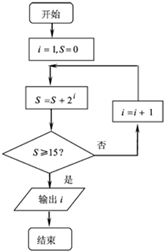

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
 如图,在平行四边形ABCD中∠DAB=60°AB=2,AD=4,将△ABC沿BD折起到△EBD的位置.
如图,在平行四边形ABCD中∠DAB=60°AB=2,AD=4,将△ABC沿BD折起到△EBD的位置.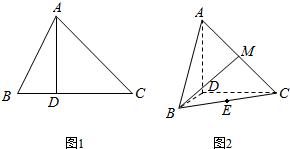 已知△ABC中,∠ACB=45°,B、C为定点且BC=3,A为动点,作AD⊥BC于D(异于点B),如图1所示.连接AB,将△ABD沿AD折起,使平面ABD⊥平面ADC,如图2所示.
已知△ABC中,∠ACB=45°,B、C为定点且BC=3,A为动点,作AD⊥BC于D(异于点B),如图1所示.连接AB,将△ABD沿AD折起,使平面ABD⊥平面ADC,如图2所示.