题目内容
【题目】位于潍坊滨海的“滨海之眼”摩天轮是世界上最高的无轴摩天轮，该摩天轮的直径均为124米，中间没有任何支撑，摩天轮顺时针匀速旋转一圈需要30分钟，当乘客乘坐摩天轮到达最高点时，距离地面145米，可以俯瞰白浪河全景，图中
与地面垂直，垂足为点
，某乘客从处进入
处的观景舱，顺时针转动
分钟后，第1次到达
点，此时点与地面的距离为114米，则
（ ）
A. 16分钟B. 18分钟C. 20分钟D. 22分钟
【答案】C
【解析】
根据摩天轮的直径和所给线段，求得OD的值；再作
，
。根据OE与OB的长度，求得
的度数，即可得
的度数，进而根据顺时针旋转即可求得经过的时间t。
根据题意，作，，如下图所示：
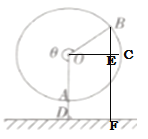
直径为
，则
，
所以
则
所以
，即
所以
因为摩天轮顺时针匀速旋转一圈需要30分钟
所以从A到B所需时间为
分钟
所以选C
练习册系列答案
相关题目
【题目】某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费
（单位：千元）对年销售量
（单位：
）和年利润
（单位：千元）的影响，对近13年的宣传费
和年销售量
数据作了初步处理，得到散点图及一些统计量的值．
由散点图知，按
建立关于的回归方程是合理的．令
，则
，经计算得如下数据：
|
|
|
|
|
|
10.15 | 109.94 | 0.16 | -2.10 | 0.21 | 21.22 |
最小二乘法求线性回归方程系数公式
（Ⅰ）根据以上信息，建立关于
的回归方程；
（Ⅱ）已知这种产品的年利润与
的关系为
．根据（1）的结果，求当年宣传费
时，年利润的预报值是多少？