题目内容
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]()

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)由![]() ,
, ![]() ,得
,得![]() 平面
平面![]() 即可证得结果;(2)设
即可证得结果;(2)设![]() ,则四棱锥
,则四棱锥![]() 的体积
的体积![]() ,解得
,解得![]() ,可得所求侧面积.
,可得所求侧面积.
试题解析:(1)由已知![]() ,得
,得![]() ,
, ![]() .
.
由于![]() ,故
,故![]() ,从而
,从而![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
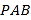
(2)在平面![]() 内作
内作![]() ,垂足为
,垂足为![]() .
.
由(1)知, ![]() 平面
平面![]() ,故
,故![]() ,可得
,可得![]() 平面
平面![]() .
.
设![]() ,则由已知可得
,则由已知可得![]() ,
, ![]() .
.
故四棱锥![]() 的体积
的体积![]() .
.
由题设得![]() ,故
,故![]() .
.
从而![]() ,
, ![]() ,
, ![]() .
.
可得四棱锥![]() 的侧面积为
的侧面积为![]() .
.
点睛:证明面面垂直,先由线线垂直证明线面垂直,再由线面垂直证明面面垂直;计算点面距离时,如直接求不方便,应首先想到转化,如平行转化、对称转化、比例转化等,找到方便求值时再计算,可以减少运算量,提高准确度,求点面距离有时能直接作出就直接求出,不方便直接求出的看成三棱锥的高,利用等体积法求出.

练习册系列答案
相关题目
