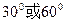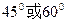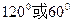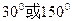题目内容
如图所示,有两条相交成60°角的直路XX′和YY′,交点是O,甲、乙分别在OX、OY上,起初甲离O点3 km,乙离O点1 km,后来两人同时用每小时4 km的速度,甲沿XX′方向,乙沿Y′Y的方向步行.
(1)起初,两人的距离是多少?
(2)用t表示t小时后两人的距离;
(3)什么时候两人的距离最短?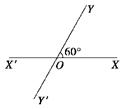
(1)起初,两人的距离是多少?
(2)用t表示t小时后两人的距离;
(3)什么时候两人的距离最短?

(1)甲、乙两人起初的距离是 km(2)|PQ|=
km(2)|PQ|=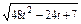 (3)在第15分钟末,两人的距离最短
(3)在第15分钟末,两人的距离最短
 km(2)|PQ|=
km(2)|PQ|=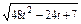 (3)在第15分钟末,两人的距离最短
(3)在第15分钟末,两人的距离最短(1)设甲、乙两人起初的位置是A、B,则由余弦定理:
|AB|2=|OA|2+|OB|2-2|OA|·|OB|·cos60°
=32+12-2×3×1×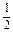 =7,∴|AB|=
=7,∴|AB|= .
.
所以甲、乙两人起初的距离是 km.
km.
(2)设甲、乙两人t小时后的位置分别是P、Q,
则|AP|=4t,|BQ|=4t,
当0≤t≤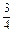 时,由余弦定理
时,由余弦定理
|PQ|2=(3-4t)2+(1+4t)2-2(3-4t)(1+4t)·cos60°,
当t>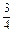 时,
时,
|PQ|2=(4t-3)2+(1+4t)2-2(4t-3)(1+4t)cos120°.
注意到上面两式实际上是统一的,
所以|PQ|2=(16t2-24t+9)+(16t2+8t+1)+(16t2-8t-3)=48t2-24t+7,
即|PQ|=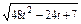 .
.
(3)∵|PQ|= ,
,
∴当t=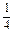 时,|PQ|的最小值是2.
时,|PQ|的最小值是2.
即在第15分钟末,两人的距离最短.
|AB|2=|OA|2+|OB|2-2|OA|·|OB|·cos60°
=32+12-2×3×1×
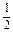 =7,∴|AB|=
=7,∴|AB|= .
.所以甲、乙两人起初的距离是
 km.
km.(2)设甲、乙两人t小时后的位置分别是P、Q,
则|AP|=4t,|BQ|=4t,
当0≤t≤
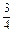 时,由余弦定理
时,由余弦定理|PQ|2=(3-4t)2+(1+4t)2-2(3-4t)(1+4t)·cos60°,
当t>
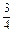 时,
时,|PQ|2=(4t-3)2+(1+4t)2-2(4t-3)(1+4t)cos120°.
注意到上面两式实际上是统一的,
所以|PQ|2=(16t2-24t+9)+(16t2+8t+1)+(16t2-8t-3)=48t2-24t+7,
即|PQ|=
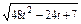 .
.(3)∵|PQ|=
 ,
,∴当t=
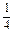 时,|PQ|的最小值是2.
时,|PQ|的最小值是2.即在第15分钟末,两人的距离最短.

练习册系列答案
相关题目
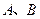 是△
是△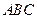 的两个内角,向量
的两个内角,向量 ,若
,若 .
. 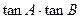 是否为定值?若为定值,请求出;否则请说明理由;
是否为定值?若为定值,请求出;否则请说明理由;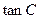 的最大值,并判断此时三角形的形状.
的最大值,并判断此时三角形的形状.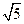 ,
,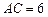 ,
,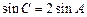 .
.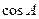 的值.
的值.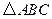 中,
中,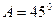 ,
, ,求其他边和角.
,求其他边和角.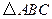 中,若
中,若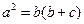 .
.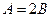 .
.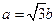 ,判断
,判断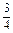 .
.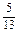 ,cosC=
,cosC=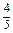 .
.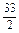 ,求BC的长.
,求BC的长. 中,
中,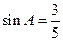 ,
,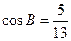 ,求
,求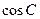 的值.
的值. 中,若
中,若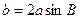 ,则
,则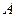 等于( )
等于( )