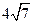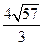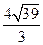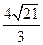题目内容
在△ABC中,cosB=-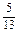 ,cosC=
,cosC=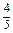 .
.
(1)求sinA的值;
(2)△ABC的面积S△ABC=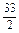 ,求BC的长.
,求BC的长.
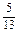 ,cosC=
,cosC=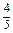 .
.(1)求sinA的值;
(2)△ABC的面积S△ABC=
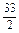 ,求BC的长.
,求BC的长.(1)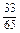 (2)
(2)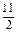
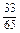 (2)
(2)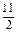
(1)由cosB=-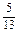 ,得sinB=
,得sinB=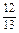 ,
,
由cosC=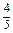 ,得sinC=
,得sinC=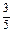 .
.
所以sinA=sin(B+C)=sinBcosC+cosBsinC=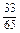 .
.
(2)由S△ABC=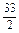 ,得
,得 ×AB×AC×sinA=
×AB×AC×sinA=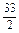 .
.
由(1)知sinA=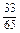 ,故AB×AC=65.
,故AB×AC=65.
又AC=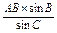 =
= AB,
AB,
故 AB2=65,AB=
AB2=65,AB=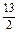 .
.
所以BC= =
=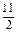 .
.
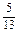 ,得sinB=
,得sinB=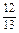 ,
,由cosC=
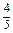 ,得sinC=
,得sinC=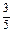 .
.所以sinA=sin(B+C)=sinBcosC+cosBsinC=
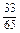 .
.(2)由S△ABC=
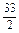 ,得
,得 ×AB×AC×sinA=
×AB×AC×sinA=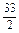 .
. 由(1)知sinA=
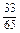 ,故AB×AC=65.
,故AB×AC=65.又AC=
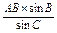 =
= AB,
AB,故
 AB2=65,AB=
AB2=65,AB=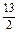 .
.所以BC=
 =
=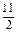 .
.
练习册系列答案
相关题目
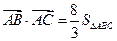 (其中S△ABC为△ABC的面积).
(其中S△ABC为△ABC的面积).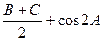 ;
; 中,角A,B,C对应的边分别为a,b,c,
中,角A,B,C对应的边分别为a,b,c,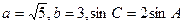 (Ⅰ)求c的值。 (Ⅱ)求
(Ⅰ)求c的值。 (Ⅱ)求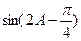 的值。
的值。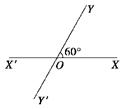
 求AC的长度越短越好,求AC最短为多少米?且当AC最短时,BC长度为多少米?
求AC的长度越短越好,求AC最短为多少米?且当AC最短时,BC长度为多少米? 三个内角
三个内角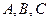 的对边分别为
的对边分别为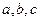 ,
, ,且
,且 .
.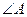 的度数;
的度数; ,
,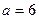 ,求
,求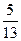 ,求这个三角形的顶角的正弦、余弦及正切值.
,求这个三角形的顶角的正弦、余弦及正切值.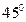 ,从甲楼顶望乙楼顶俯角为
,从甲楼顶望乙楼顶俯角为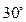 ,则甲、乙两楼的高度分别为____________________.
,则甲、乙两楼的高度分别为____________________. 中,若
中,若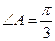 ,AC=2,
,AC=2,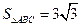 ,则
,则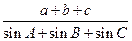 的值为( ).
的值为( ).