题目内容
3.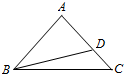 如图,在△ABC中,AB=AC,D在线段AC上,且AC=$\sqrt{2}$AD,BD=1.
如图,在△ABC中,AB=AC,D在线段AC上,且AC=$\sqrt{2}$AD,BD=1.(Ⅰ)若A=$\frac{π}{2}$,求sin∠DBC的值;
(Ⅱ)求△ABC面积的最大值.
分析 (Ⅰ)设出AD,利用勾股定理求得AD,进而求得sin∠ABD和cos∠ABD,利用sin∠DBC=sin($\frac{π}{4}$-∠ABD)求得sin∠DBC的值.
(Ⅱ)设出AD,利用余弦定理表示出cos∠BAD,进而表示出sin∠BAC,最后利用三角形面积公式表示出三角形的面积,利用二次函数的性质求得面积最大值.
解答 解:(Ⅰ)设AD=x,AB=$\sqrt{2}$x,
∵x2+2x2=1,
∴x=$\frac{\sqrt{3}}{3}$,
即AD=$\frac{\sqrt{3}}{3}$,AB=$\frac{\sqrt{6}}{3}$.
sin∠ABD=$\frac{\sqrt{3}}{3}$,cos∠ABD=$\frac{\sqrt{6}}{3}$,
sin∠DBC=sin($\frac{π}{4}$-∠ABD)=$\frac{\sqrt{2}}{2}$×$\frac{\sqrt{6}}{3}$-$\frac{\sqrt{2}}{2}$×$\frac{\sqrt{3}}{3}$=$\frac{2\sqrt{3}-\sqrt{6}}{6}$.
(Ⅱ)设AD=x,AB=$\sqrt{2}$x,
在△ABD中,由余弦定理得cos∠BAD=$\frac{{x}^{2}+2{x}^{2}-1}{2\sqrt{2}{x}^{2}}$=$\frac{3{x}^{2}-1}{2\sqrt{2}{x}^{2}}$,
sin∠BAC=$\sqrt{1-co{s}^{2}∠BAD}$=$\frac{\sqrt{-({x}^{2}-3)^{2}+8}}{2\sqrt{2}{x}^{2}}$,
S△ABC=$\frac{1}{2}$•2x2•$\frac{\sqrt{-({x}^{2}-3)^{2}+8}}{2\sqrt{2}{x}^{2}}$=$\frac{\sqrt{-({x}^{2}-3)^{2}+8}}{2\sqrt{2}}$,
当x=$\sqrt{3}$时,三角形面积有最大值1.
点评 本题主要考查了两角和公式的运用,余弦定理的运用.考查了学生的转化与化归的思想.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | ①③ | B. | ②⑤ | C. | ③⑤ | D. | ②④ |