题目内容
12.已知在直角坐标系xOy中,曲线C的参数方程为$\left\{\begin{array}{l}x=cosθ\\ y=2sinθ\end{array}$(θ为参数),点P在曲线C上,以Ox为极轴建立极坐标系,点Q的极坐标为($\sqrt{3}$,$\frac{π}{2}$),则P,Q两点距离的最大值为2+$\sqrt{3}$.分析 将Q的坐标化为直角坐标,由两点的距离公式,结合三角函数的同角公式和配方法,以及正弦函数的值域,即可得到最大值.
解答 解:设P(cosθ,2sinθ),
Q($\sqrt{3}$,$\frac{π}{2}$)化为直角坐标为Q(0,$\sqrt{3}$),
即有|PQ|=$\sqrt{(cosθ-0)^{2}+(2sinθ-\sqrt{3})^{2}}$
=$\sqrt{co{s}^{2}θ+4si{n}^{2}θ-4\sqrt{3}sinθ+3}$
=$\sqrt{3si{n}^{2}θ-4\sqrt{3}sinθ+4}$=|$\sqrt{3}$sinθ-2|,
由-1≤sinθ≤1,
即有sinθ=-1,|PQ|取得最大值2+$\sqrt{3}$.
故答案为:2+$\sqrt{3}$.
点评 本题考查极坐标和直角坐标的互化,考查椭圆的参数方程的运用,同时考查三角函数的化简和求值,运用正弦函数的值域是解题的关键.

练习册系列答案
相关题目
20.下列不等式正确的是( )
| A. | sin1<2sin$\frac{1}{2}<3sin\frac{1}{3}$ | B. | 3sin$\frac{1}{3}<2sin\frac{1}{2}$<sin1 | ||
| C. | sin1<3sin$\frac{1}{3}<2sin\frac{1}{2}$ | D. | 2sin$\frac{1}{2}<sin1<3sin\frac{1}{3}$ |
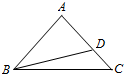 如图,在△ABC中,AB=AC,D在线段AC上,且AC=$\sqrt{2}$AD,BD=1.
如图,在△ABC中,AB=AC,D在线段AC上,且AC=$\sqrt{2}$AD,BD=1. (1)求⊙P的半径(用θ表示);
(1)求⊙P的半径(用θ表示);