题目内容
8.已知函数①f(x)=x+1;②f(x)=2x-2;③f(x)=$\frac{1}{x}$;④f(x)=lnx;⑤f(x)=cosx;其中对于f(x)定义域内的任意x1,都存在x2,使得f(x1)f(x2)=-x1x2成立的函数是( )| A. | ①③ | B. | ②⑤ | C. | ③⑤ | D. | ②④ |
分析 由题意得到对函数f(x)图象上任意一点A(x1,f(x1)),都存在一点B(x2,f(x2)),使OA⊥OB,对于①根据斜率即可判断,对于③④利用反证即可证明,对于②⑤举例即可.
解答 解:由f(x1)f(x2)+x1x2=0知,对函数f(x)图象上任意一点A(x1,f(x1)),
都存在一点B(x2,f(x2)),使OA⊥OB,若斜率存在则kOAkOB=-1,
对于①f(x)=x+1,无论两个点如何取,OA和OB的斜率均等于1,故①不成立,
对于②f(x)=2x-2;若x1=1,则f(x1)=0,若x2=0,则f(x2)=-1,则f(x1)f(x2)=-x1x2成立,故②成立;
对于③f(x)=$\frac{1}{x}$;若f(x1)f(x2)=$\frac{1}{{x}_{1}•{x}_{2}}$=-x1x2⇒(x1x2)2=-1,不成立,故③不成立;
对于④f(x)=lnx,则f′(x)=$\frac{1}{x}$;kOA=$\frac{1}{{x}_{1}}$,kOB=$\frac{1}{{x}_{2}}$,则kOAkOB=$\frac{1}{{x}_{1}{x}_{2}}$>0,故④不成立,
对于⑤f(x)=cosx,若x1=0,则f(x1)=1,若x2=$\frac{π}{2}$,则f(x2)=0,则f(x1)f(x2)=-x1x2成立,故⑤成立;
符合条件的有②⑤;
故选:B.
点评 本题考查了常见函数的图象和性质,以及反证法,属于中档题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
18.已知函数f(x)=$\left\{\begin{array}{l}3,x≥m\\{x}^{2}+5x-12,x<m\end{array}\right.$,若函数g(x)=f(x)-x恰有三个不同的零点,则实数m的取值范围是( )
| A. | m<2 | B. | 2<m≤3 | C. | 2≤m≤3 | D. | m>3 |
16.在等差数列{an}中,a9=$\frac{1}{2}$a12+6,则该数列的前11项和为( )
| A. | 12 | B. | 72 | C. | 132 | D. | 192 |
20.下列不等式正确的是( )
| A. | sin1<2sin$\frac{1}{2}<3sin\frac{1}{3}$ | B. | 3sin$\frac{1}{3}<2sin\frac{1}{2}$<sin1 | ||
| C. | sin1<3sin$\frac{1}{3}<2sin\frac{1}{2}$ | D. | 2sin$\frac{1}{2}<sin1<3sin\frac{1}{3}$ |
 如图,斜三棱柱ABC-A1B1C1中,A1B1=A1C1,点E,F分别是B1C1,A1B1的中点,AA1=AB=BE=1,∠A1AB=60°.
如图,斜三棱柱ABC-A1B1C1中,A1B1=A1C1,点E,F分别是B1C1,A1B1的中点,AA1=AB=BE=1,∠A1AB=60°.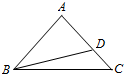 如图,在△ABC中,AB=AC,D在线段AC上,且AC=$\sqrt{2}$AD,BD=1.
如图,在△ABC中,AB=AC,D在线段AC上,且AC=$\sqrt{2}$AD,BD=1.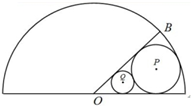 (1)求⊙P的半径(用θ表示);
(1)求⊙P的半径(用θ表示);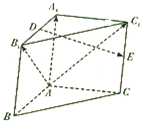 如图,在三棱柱ABC-A1B1C1中,A1A⊥底面ABC,AB⊥AC,E分别是A1B1,CC1的中点.
如图,在三棱柱ABC-A1B1C1中,A1A⊥底面ABC,AB⊥AC,E分别是A1B1,CC1的中点.