题目内容
18．已知（$\root{3}{y}$+$\sqrt{x}$）5的二次展开式的第三项为10，则y关于x的函数图象大致形状为（ ）| A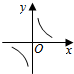． |  | B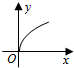． |  | C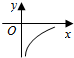． |  | D． |  |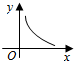
分析 先由二项式定理展开式的通项公式，求出展开式中的第三项，从而得到y关于x的函数，再根据此函数的图象性质作出判断即可．
解答 解：∵（$\root{3}{y}$+$\sqrt{x}$）5的展开式的第r+1项Tr+1=C5r${y}^{\frac{5-r}{3}}$${x}^{\frac{r}{2}}$ （x≥0）
∴展开式的第三项为C52yx=10xy=10，
∴xy=1，即y=$\frac{1}{x}$（x＞0），
∴则y关于x的函数为y=$\frac{1}{x}$（x＞0），
其图象为双曲线y=$\frac{1}{x}$的一支，位于第一象限，
故选：D．
点评 本题综合考察了二项式定理及函数的图象和性质，反比例函数的图象和性质．
练习册系列答案
阅读快车系列答案
相关题目
6．从抛物线y2=4x图象上一点P引抛物线准线的垂线，垂足为M，且|PM|=3，设抛物线焦点为F，则△MPF周长为（ ）
| A． | 6+3$\sqrt{2}$ | B． | 5+2$\sqrt{3}$ | C． | 8 | D． | 6+2$\sqrt{3}$ |
13．
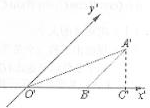如图是利用斜二测画法画出的△ABO的直观图，已知O′B′=4，且△ABO的面积为16，过A′作A′C′⊥x′轴，则A′C′的长为（ ）
如图是利用斜二测画法画出的△ABO的直观图，已知O′B′=4，且△ABO的面积为16，过A′作A′C′⊥x′轴，则A′C′的长为（ ）| A． | $2\sqrt{2}$ | B． | $\sqrt{2}$ | C． | $16\sqrt{2}$ | D． | 1 |
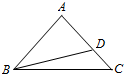如图，在△ABC中，AB=AC，D在线段AC上，且AC=$\sqrt{2}$AD，BD=1．
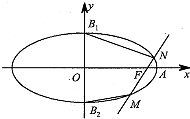已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0），其右顶点为 A（2，0），上、下顶点分别为 B1，B2．直线 A B2的斜率为$\frac{1}{2}$，过椭圆的右焦点F的直线交椭圆于 M，N两点（ M，N均在y轴右侧）．