题目内容
11.如图,矩形ABCD中,AB=3,BC=4.E、F分别在线段BC和AD上,EF∥AB,将矩形ABEF沿EF折起.记折起后的矩形为MNEF,且平面MNEF⊥平面ECDF.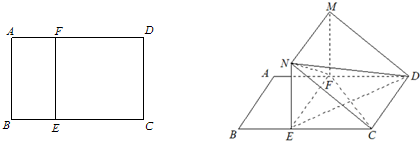
(Ⅰ)求证:NC∥平面MFD;
(Ⅱ)求四面体NFEC体积的最大值,并求此时D点到平面CFN的距离.
分析 (Ⅰ)由四边形MNEF、EFDC都是矩形,证得四边形MNCD是平行四边形,从而得到NC∥MD,再由线面平行的判定得答案;
(Ⅱ)设NE=x,则EC=4-x,其中0<x<4,写出四面体NFEC的体积为${V}_{NFEC}=\frac{1}{3}{S}_{△FEC}•NE=\frac{1}{3}•(\frac{1}{2}•(4-x)•3)x$=$-\frac{1}{2}{x}^{2}+2x$,利用二次函数知识可得当x=2时,四面体的体积最大,设出D到平面CFN的距离为h,通过解直角三角形求得FN=FC=$\sqrt{{2}^{2}+{3}^{2}}=\sqrt{13}$,NC=$\sqrt{{2}^{2}+{2}^{2}}=2\sqrt{2}$,得到S△CFN,由VN-DFC=VD-NFC列式求得得$h=\frac{6}{\sqrt{22}}=\frac{3\sqrt{22}}{11}$.
解答 (Ⅰ)证明:如图,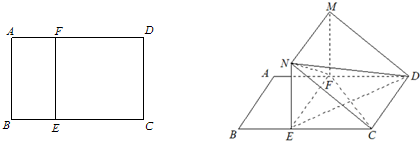 ∵四边形MNEF、EFDC都是矩形,
∵四边形MNEF、EFDC都是矩形,
∴MN∥EF∥CD,MN=EF=CD,
∴四边形MNCD是平行四边形,则NC∥MD,
∵NC?平面MFD,MD?平面MFD,
∴NC∥平面MFD;
(Ⅱ)解:设NE=x,则EC=4-x,其中0<x<4,由条件可知NE⊥平面FEC,
∴四面体NFEC的体积为${V}_{NFEC}=\frac{1}{3}{S}_{△FEC}•NE=\frac{1}{3}•(\frac{1}{2}•(4-x)•3)x$=$-\frac{1}{2}{x}^{2}+2x$.
∴当x=2时,四面体的体积最大,且(VN-FEC)max=2.
由题意可知,四边形EFDC为矩形,∴S△EFC=S△DFC,故VN-EFC=VN-DFC,
设D到平面CFN的距离为h,在△CFN中,FN=FC=$\sqrt{{2}^{2}+{3}^{2}}=\sqrt{13}$,NC=$\sqrt{{2}^{2}+{2}^{2}}=2\sqrt{2}$,
∴${S}_{△CFN}=\frac{1}{2}×2\sqrt{2}×\sqrt{(\sqrt{13})^{2}-(\sqrt{2})^{2}}=\sqrt{22}$.
由${V}_{N-DFC}={V}_{D-NFC}=\frac{1}{3}{S}_{△CFN}•h=2$,得$h=\frac{6}{\sqrt{22}}=\frac{3\sqrt{22}}{11}$.
点评 本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力,关键是注意折叠问题折叠前后的变量和不变量,是中档题.

| A. | {1,2,3} | B. | {1,3,5} | C. | {2,3,5} | D. | {1,3,5,7} |
| A. | 6+3$\sqrt{2}$ | B. | 5+2$\sqrt{3}$ | C. | 8 | D. | 6+2$\sqrt{3}$ |
| A. | 12 | B. | 72 | C. | 132 | D. | 192 |
| A. | sin1<2sin$\frac{1}{2}<3sin\frac{1}{3}$ | B. | 3sin$\frac{1}{3}<2sin\frac{1}{2}$<sin1 | ||
| C. | sin1<3sin$\frac{1}{3}<2sin\frac{1}{2}$ | D. | 2sin$\frac{1}{2}<sin1<3sin\frac{1}{3}$ |
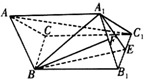 如图,斜三棱柱ABC-A1B1C1中,A1B1=A1C1,点E,F分别是B1C1,A1B1的中点,AA1=AB=BE=1,∠A1AB=60°.
如图,斜三棱柱ABC-A1B1C1中,A1B1=A1C1,点E,F分别是B1C1,A1B1的中点,AA1=AB=BE=1,∠A1AB=60°.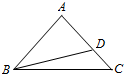 如图,在△ABC中,AB=AC,D在线段AC上,且AC=$\sqrt{2}$AD,BD=1.
如图,在△ABC中,AB=AC,D在线段AC上,且AC=$\sqrt{2}$AD,BD=1.