定义运算:$|\begin{array}{l}{{a} {1}}&{{a} {2}}\\{{a} {3}}&{{a} {4}}\end{array}|$=a1a4-a2a3.已知函数f(x)=$|\begin{array}{l}{sinx}&{-1}\\{1}&{cosx}\end{array}|$.则函数fA．$\frac{π}{2}$B．πC．2πD．4π 题目和参考答案——青夏教育精英家教网—

题目内容

16．定义运算：$|\begin{array}{l}{{a}_{1}}&{{a}_{2}}\\{{a}_{3}}&{{a}_{4}}\end{array}|$=a₁a₄-a₂a₃，已知函数f（x）=$|\begin{array}{l}{sinx}&{-1}\\{1}&{cosx}\end{array}|$，则函数f（x）的最小正周期是（　　）

A．

$\frac{π}{2}$

B．

C．

2π

D．

4π

分析由运算定义及二倍角的正弦函数公式可求f（x），根据三角函数的周期性及其求法即可得解．

解答解：由题意可得：f（x）=$|\begin{array}{l}{sinx}&{-1}\\{1}&{cosx}\end{array}|$=sinxcosx+1=$\frac{1}{2}$sin2x+1，
从而可得：函数f（x）的最小正周期T=$\frac{2π}{2}$=π．
故选：B．

点评本题主要考查了二倍角的正弦函数公式，三角函数的周期性及其求法，属于基本知识的考查．

练习册系列答案

相关题目

3．

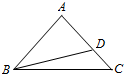如图，在△ABC中，AB=AC，D在线段AC上，且AC=$\sqrt{2}$AD，BD=1．
（Ⅰ）若A=$\frac{π}{2}$，求sin∠DBC的值；
（Ⅱ）求△ABC面积的最大值．

4．点F是抛物线T：x²=2py（y＞0）的焦点，F₁是双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点，若线段FF₁的中点P恰为抛物线T与双曲线C的渐近线在第一象限内的交点，则双曲线C的离心率e=$\frac{3\sqrt{2}}{4}$．

4．在平面直角坐标系xOy中，椭圆C：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的离心率为$\frac{{2\sqrt{2}}}{3}$，长轴长为6．
（I）求椭圆C的方程；
（Ⅱ）过原点的直线与椭圆C交于A，B两点（A，B不是椭圆C的顶点）．点D在椭圆C上，且AD⊥AB，直线BD与x轴、y轴分别交于M，N两点．
（i）设直线BD，AM的斜率分别为k₁，k₂，证明存在常数λ使得k₁=λk₂，并求出λ的值；
（ii）求△OMN面积的最大值．

11．

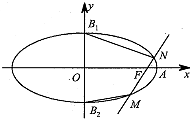已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0），其右顶点为 A（2，0），上、下顶点分别为 B₁，B₂．直线 A B₂的斜率为$\frac{1}{2}$，过椭圆的右焦点F的直线交椭圆于 M，N两点（ M，N均在y轴右侧）．
（Ⅰ）求椭圆的方程；
（Ⅱ）设四边形 M N B₁ B₂面积为S，求S的取值范围．

1．

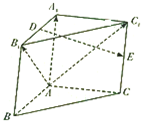如图，在三棱柱ABC-A₁B₁C₁中，A₁A⊥底面ABC，AB⊥AC，E分别是A₁B₁，CC₁的中点．
（Ⅰ）用基向量$\overrightarrow{A{A}_{1}}$，$\overrightarrow{A{B}_{1}}$，$\overrightarrow{A{C}_{1}}$表示向量$\overrightarrow{DE}$；
（Ⅱ）若AB=AC=AA₁=1，求直线DE与平面AB₁C₁所成角的正弦值．

8．已知圆M：x²+y²+x-6y+m=0
（Ⅰ）当m=$\frac{1}{4}$，过N（-$\frac{3}{2}$，-1）的直线a与圆的相交所得的弦长为4$\sqrt{2}$，求直线a的方程；
（Ⅱ）设直线l：x+2y-3=0与圆M交于P，Q两点，且与PQ为直径的圆恰好经过原点O，求m的值；
（Ⅲ）当m=$\frac{1}{4}$时，直线4x-3y-12=0与x，y轴分别交于A，B两点，在圆M上是否存在点C，使得△ABC的面积为$\frac{23}{2}$，若存在，请指出点C的个数，若不存在，请说明理由．

5．已知函数f（x）=$\frac{sin2x-cos2x+1}{2sinx}$．
（1）求函数f（x）的定义域；
（2）求函数f（x）的值域．

6．

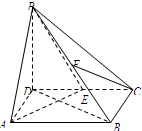如图，在四棱锥P-ABCD中，底面ABCD是矩形，AB=2，AD=$\sqrt{2}$，PD⊥平面ABCD，E，F分别为CD，PB的中点．求证：
（1）CF∥平面PAE；
（2）AE⊥平面PBD．

试题分类