题目内容
已知a为实数,函数f(x)=(x2+1)(x+a),若f′(-1)=0,求函数y=f(x)在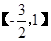 上的最大值和最小值.
上的最大值和最小值.
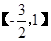 上的最大值和最小值.
上的最大值和最小值.f(x)在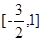 上的最大值为f(1)=6,最小值为f
上的最大值为f(1)=6,最小值为f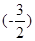 =
=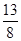
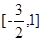 上的最大值为f(1)=6,最小值为f
上的最大值为f(1)=6,最小值为f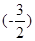 =
=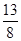
试题分析:解: f′(x)=3x2+2ax+1. ..1分
∵f′(-1)=0,∴3-2a+1=0,即a=2 1分
∴f′(x)=3x2+4x+1=3
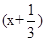 (x+1).
(x+1).由f′(x)≥0,得x≤-1或x≥-
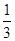 ;由f′(x)≤0,得-1≤x≤-
;由f′(x)≤0,得-1≤x≤-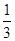
因此,函数f(x)的单调递增区间为
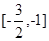 和
和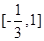 ,
,单调递减区间为
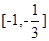 4分
4分∴f(x)在x=-1取得极大值f(-1)=2,
f(x)在x=-
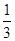 取得极小值f
取得极小值f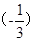 =
=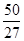 .
.又∵f
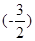 =
=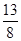 ,f(1)=6,且
,f(1)=6,且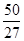 >
>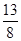 ,
,∴f(x)在
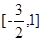 上的最大值为f(1)=6,最小值为f
上的最大值为f(1)=6,最小值为f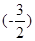 =
=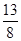 4分
4分点评:主要是考查了函数的单调性的判定和求解最值的运用,属于基础题。

练习册系列答案
相关题目
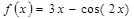 在
在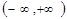 上( )
上( )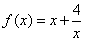 的单调递减区间为________
的单调递减区间为________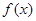 满足
满足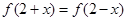 ,且
,且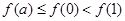 ,则实数
,则实数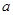 的取值范围是_________.
的取值范围是_________.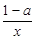 -1.
-1. 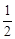 时, 求函数f(x)的单调区间;
时, 求函数f(x)的单调区间;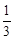 时, 设函数g(x)=x2-2bx-
时, 设函数g(x)=x2-2bx-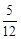 , 若对于
, 若对于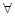 x1∈
x1∈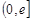 ,
, 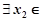 [0, 1]使f(x1)≥g(x2)成立, 求实数b的取值范围.(e是自然对数的底, e<
[0, 1]使f(x1)≥g(x2)成立, 求实数b的取值范围.(e是自然对数的底, e<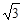 +1).
+1). 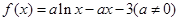 .
.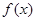 的单调区间
的单调区间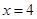 处切线的斜率为
处切线的斜率为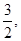 若函数
若函数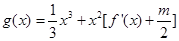 在区间(1,3)上不是单调函数,求m的取值范围
在区间(1,3)上不是单调函数,求m的取值范围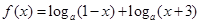 ,其中
,其中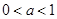 ,记函数
,记函数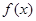 的定义域为D.
的定义域为D.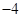 ,求
,求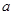 的值;
的值;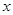 ,不等式
,不等式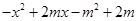 <
<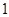 恒成立,求实数
恒成立,求实数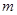 的取值范围.
的取值范围.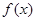
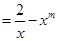 ,且
,且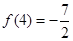
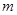 的值
的值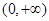 上的单调性,并利用定义给出证明
上的单调性,并利用定义给出证明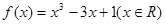 。
。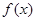 在点
在点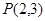 处的切线方程;
处的切线方程;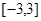 的最大值与最小值。
的最大值与最小值。