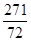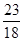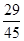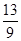题目内容
已知函数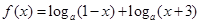 ,其中
,其中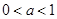 ,记函数
,记函数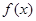 的定义域为D.
的定义域为D.
(1)求函数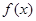 的定义域D;
的定义域D;
(2)若函数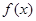 的最小值为
的最小值为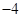 ,求
,求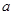 的值;
的值;
(3)若对于D内的任意实数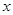 ,不等式
,不等式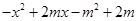 <
<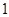 恒成立,求实数
恒成立,求实数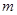 的取值范围.
的取值范围.
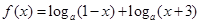 ,其中
,其中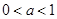 ,记函数
,记函数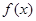 的定义域为D.
的定义域为D.(1)求函数
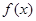 的定义域D;
的定义域D;(2)若函数
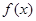 的最小值为
的最小值为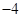 ,求
,求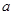 的值;
的值;(3)若对于D内的任意实数
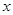 ,不等式
,不等式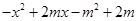 <
<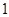 恒成立,求实数
恒成立,求实数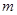 的取值范围.
的取值范围.(1)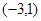
(2)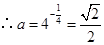
(3) (-∞,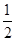 )∪[
)∪[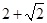 ,+∞)
,+∞)
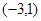
(2)
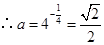
(3) (-∞,
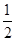 )∪[
)∪[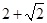 ,+∞)
,+∞)试题分析:解:(1)要使函数有意义:则有
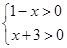 ,解得
,解得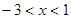
∴ 函数的定义域D为
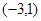 2分
2分(2)
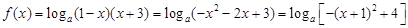
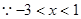
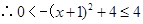
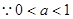 ,
,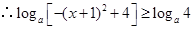 ,即
,即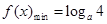 , 5分
, 5分由
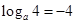 ,得
,得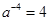 ,
,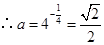 . 7分
. 7分(注:
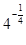 不化简为
不化简为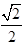 扣1分)
扣1分)(3)由题知-x2+2mx-m2+2m<1在x∈
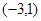 上恒成立,
上恒成立,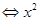 -2mx+m2-2m+1>0在x∈
-2mx+m2-2m+1>0在x∈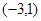 上恒成立, 8分
上恒成立, 8分令g(x)=x2-2mx+m2-2m+1,x∈
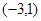 ,
,配方得g(x)=(x-m)2-2m+1,其对称轴为x=m,
当m≤-3时, g(x)在
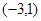 为增函数,
为增函数,∴g(-3)= (-3-m)2-2m+1= m2+4m +10≥0,
而m2+4m +10≥0对任意实数m恒成立,∴m≤-3. 10分
②当-3<m<1时,函数g(x)在(-3,-1)为减函数,在(-1, 1)为增函数,
∴g(m)=-2m+1>0,解得m<
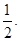 ∴-3<m<
∴-3<m<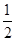 12分
12分③当m≥1时,函数g(x)在
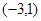 为减函数,∴g(1)= (1-m)2-2m+1= m2-4m +2≥0,
为减函数,∴g(1)= (1-m)2-2m+1= m2-4m +2≥0,解得m≥
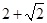 或m≤
或m≤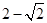 , ∴-3<m<
, ∴-3<m<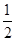 14分
14分综上可得,实数m的取值范围是 (-∞,
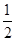 )∪[
)∪[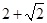 ,+∞) 16分
,+∞) 16分点评:解决的关键是利用函数的概念以及分离参数的思想来借助于二次函数的最值得到参数的范围。属于基础题。

练习册系列答案
相关题目
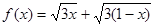 的最大值为
的最大值为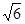
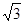
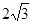
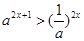 ,其中
,其中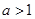 ,则
,则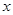 的取值范围是 .
的取值范围是 .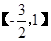 上的最大值和最小值.
上的最大值和最小值.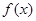 是偶函数,对
是偶函数,对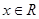 都有
都有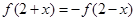 ,当
,当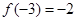 时f (2013)的值为 .
时f (2013)的值为 .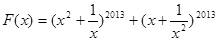 在区间
在区间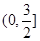 上的最小值为 .
上的最小值为 .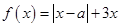 ,其中
,其中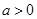 .
.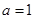 时,求不等式
时,求不等式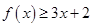 的解集;
的解集;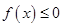 的解集为
的解集为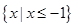 ,求
,求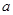 的值.
的值.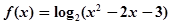 ,给定区间E,对任意
,给定区间E,对任意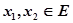 ,当
,当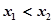 时,总有
时,总有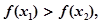 则下列区间可作为E的是( )
则下列区间可作为E的是( )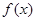 与
与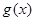 ,若区间
,若区间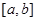 上
上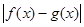 的最大值称为
的最大值称为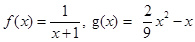 在
在 上的“绝对差”为
上的“绝对差”为