题目内容
设函数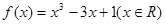 。
。
(1)求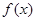 在点
在点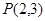 处的切线方程;
处的切线方程;
(2)求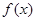 在区间
在区间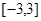 的最大值与最小值。
的最大值与最小值。
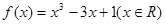 。
。(1)求
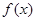 在点
在点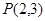 处的切线方程;
处的切线方程;(2)求
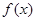 在区间
在区间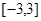 的最大值与最小值。
的最大值与最小值。(1)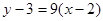 (2)
(2)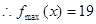 ,
,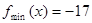
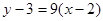 (2)
(2)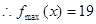 ,
,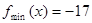
试题分析:解:(1)
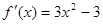 2
2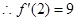 3
3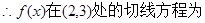
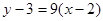 5
5得
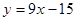 6
6(2)
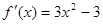
令
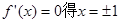 7
7又
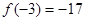
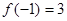
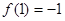
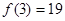 11
11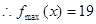
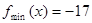 13
13点评:主要是考查导数的几何意义求解切线方程,以及导数的符号判定单调性得到最值,属于基础题。

练习册系列答案
相关题目
 ,且
,且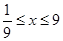 .
. 的值;
的值;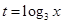 ,求
,求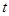 取值范围;
取值范围;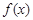 表示成以
表示成以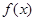 的最大值与最小值及与之对应的x的值.
的最大值与最小值及与之对应的x的值.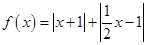 .
.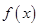 的图象,写出函数
的图象,写出函数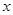 的不等式
的不等式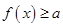
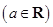 .
.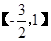 上的最大值和最小值.
上的最大值和最小值.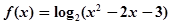 ,给定区间E,对任意
,给定区间E,对任意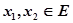 ,当
,当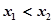 时,总有
时,总有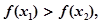 则下列区间可作为E的是( )
则下列区间可作为E的是( )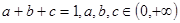 ,求证:
,求证: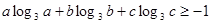 ;
;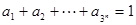 ,
,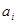 >0(i=1,2,3,…,3n),求证:
>0(i=1,2,3,…,3n),求证: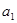
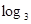
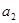
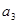
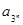
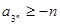
 (2-ax)在[0,1]上是减函数,则a的取值范围是
(2-ax)在[0,1]上是减函数,则a的取值范围是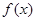 与
与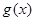 ,若区间
,若区间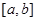 上
上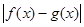 的最大值称为
的最大值称为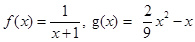 在
在 上的“绝对差”为
上的“绝对差”为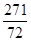
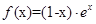 的单调递减区间 .
的单调递减区间 .