题目内容
已知函数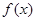
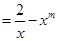 ,且
,且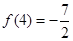
(1)求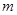 的值
的值
(2)判断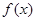 在
在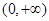 上的单调性,并利用定义给出证明
上的单调性,并利用定义给出证明
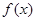
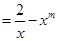 ,且
,且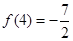
(1)求
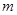 的值
的值(2)判断
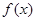 在
在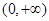 上的单调性,并利用定义给出证明
上的单调性,并利用定义给出证明(1)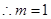
(2)设变量,作差,变形,定号,下结论,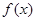 在
在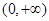 上单调递减
上单调递减
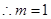
(2)设变量,作差,变形,定号,下结论,
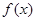 在
在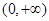 上单调递减
上单调递减试题分析:解:(1)
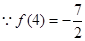
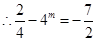
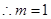 4分
4分(2)
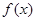
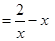 在
在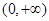 上单调递减 5分
上单调递减 5分证明如下:
任取
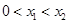 ,则
,则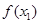
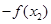 =
=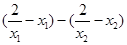 =
=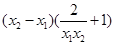 8分
8分∵
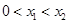
∴
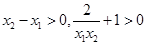
∴
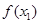
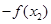 >0,即
>0,即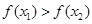
∴
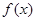 在
在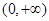 上单调递减 12分
上单调递减 12分考点:函数的单调性
点评:解决的关键是能根据函数单调性的定义来加以证明,同时求解函数值,属于基础题。

练习册系列答案
相关题目
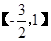 上的最大值和最小值.
上的最大值和最小值.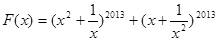 在区间
在区间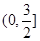 上的最小值为 .
上的最小值为 .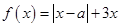 ,其中
,其中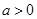 .
.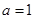 时,求不等式
时,求不等式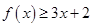 的解集;
的解集;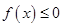 的解集为
的解集为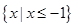 ,求
,求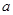 的值.
的值.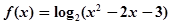 ,给定区间E,对任意
,给定区间E,对任意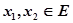 ,当
,当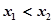 时,总有
时,总有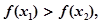 则下列区间可作为E的是( )
则下列区间可作为E的是( )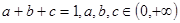 ,求证:
,求证: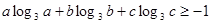 ;
;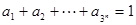 ,
,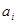 >0(i=1,2,3,…,3n),求证:
>0(i=1,2,3,…,3n),求证: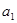
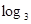
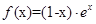 的单调递减区间 .
的单调递减区间 .