题目内容
设中心在原点的双曲线与椭圆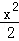 +y2=1有公共的焦点,且它们的离心率互为倒数,则该双曲线的方程是 .
+y2=1有公共的焦点,且它们的离心率互为倒数,则该双曲线的方程是 .
2x2﹣2y2=1
解析试题分析:椭圆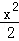 +y2=1中c=1
+y2=1中c=1
∵中心在原点的双曲线与椭圆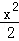 +y2=1有公共的焦点
+y2=1有公共的焦点
∴双曲线中c=1,
∵椭圆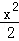 +y2=1的离心率为
+y2=1的离心率为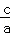 =
=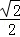 ,椭圆与双曲线的离心率互为倒数.
,椭圆与双曲线的离心率互为倒数.
∴双曲线的离心率为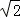 ,
,
∴双曲线中a=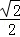 ,b2=c2﹣a2=
,b2=c2﹣a2=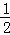 ,b=
,b=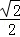
∴双曲线的方程为2x2﹣2y2=1
故答案为2x2﹣2y2=1.
考点:双曲线的标准方程;椭圆的简单性质;双曲线的简单性质
点评:本题主要考查了双曲线的性质和椭圆的标准方程.要记住双曲线和椭圆的定义和性质,解答直线AB的斜率的关键是利用方程组思想.

练习册系列答案
相关题目
 中,抛物线
中,抛物线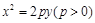 上纵坐标为1的一点到焦点的距离为3,则焦点到准线的距离为 .
上纵坐标为1的一点到焦点的距离为3,则焦点到准线的距离为 .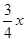 ,焦点到渐近线的距离为3,则该双曲线的方程为______
,焦点到渐近线的距离为3,则该双曲线的方程为______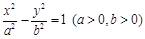 与抛物线
与抛物线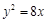 有一个公共的焦点,且双曲线上的点到坐标原点的最短距离为1,则该双曲线的标准方程是___________。
有一个公共的焦点,且双曲线上的点到坐标原点的最短距离为1,则该双曲线的标准方程是___________。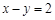 与抛物线
与抛物线 交于
交于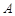 、
、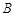 两点,则线段
两点,则线段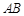 的中点坐标是______.
的中点坐标是______.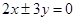 为渐近线,且经过点
为渐近线,且经过点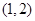 的双曲线标准方程是
的双曲线标准方程是 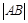 为C的实轴长的2倍,则C的离心率为_________.
为C的实轴长的2倍,则C的离心率为_________.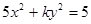 的一个焦点是
的一个焦点是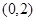 ,那么
,那么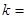 .
.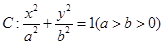 的左焦点为
的左焦点为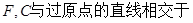
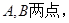
 .
.