题目内容
设直线l过线C的一个焦点,且与C的一条对称轴垂直,l与C交于A,B两点,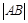 为C的实轴长的2倍,则C的离心率为_________.
为C的实轴长的2倍,则C的离心率为_________.
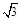
解析试题分析:设双曲线C: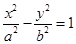 ,焦点F(-c,0),对称轴y=0,由题设知
,焦点F(-c,0),对称轴y=0,由题设知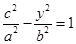 ,y=±
,y=±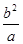 ,∴
,∴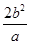 =4a,b2=2a2,即c2-a2=2a2,所以c2=3a2,∴e=
=4a,b2=2a2,即c2-a2=2a2,所以c2=3a2,∴e=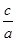 =
=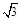 .
.
考点:本题考查了双曲线离心率的求法
点评:本题中弦AB为双曲线的通径,其长度为定值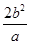 ,同学们在解答客观题时可灵活运用
,同学们在解答客观题时可灵活运用

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
已知椭圆C1的中心在原点、焦点在x轴上,抛物线C2的顶点在原点、焦点在x轴上。小明从曲线C1,C2上各取若干个点(每条曲线上至少取两个点),并记录其坐标(x,y)。由于记录失误,使得其中恰好有一个点既不在椭圆上C1上,也不在抛物线C2上。小明的记录如下:
| X | -2 | -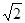 | 0 | 2 | 2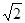 | 3 |
| Y | 2 | 0 | 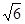 | -2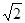 | 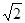 | -2 |
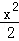 +y2=1有公共的焦点,且它们的离心率互为倒数,则该双曲线的方程是 .
+y2=1有公共的焦点,且它们的离心率互为倒数,则该双曲线的方程是 .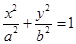 (a>b>0)的左、右顶点分别是A,B,左、右焦点分别是F1,F2.若|AF1|,|F1F2|,|F1B|成等比数列,则此椭圆的离心率为 .
(a>b>0)的左、右顶点分别是A,B,左、右焦点分别是F1,F2.若|AF1|,|F1F2|,|F1B|成等比数列,则此椭圆的离心率为 .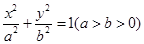 的四个顶点A、B、C、D, 若菱形ABCD的内切圆恰好经过椭圆的焦点, 则椭圆的离心率为 __ .
的四个顶点A、B、C、D, 若菱形ABCD的内切圆恰好经过椭圆的焦点, 则椭圆的离心率为 __ . ,平面上任意一点P关于斜坐标系的斜坐标这样定义:若
,平面上任意一点P关于斜坐标系的斜坐标这样定义:若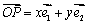 (其中
(其中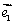 ,
,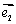 分别是x轴,y轴正方向的单位向量),则P点的斜坐标为(x,y),向量
分别是x轴,y轴正方向的单位向量),则P点的斜坐标为(x,y),向量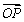 的斜坐标为(x,y).给出以下结论:
的斜坐标为(x,y).给出以下结论:
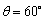 ,P(2,-1),则
,P(2,-1),则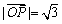 ;
;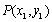 ,
,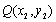 ,则
,则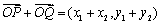 ;
;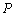 (x,y),
(x,y),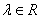 ,则
,则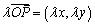 ;
;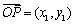 ,
,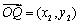 ,则
,则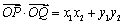 ;
;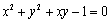 .
. 中,椭圆
中,椭圆 的中心为原点,焦点
的中心为原点,焦点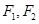 在
在  轴上,离心率为
轴上,离心率为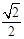 。过
。过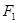 的直线
的直线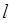 交椭圆
交椭圆 两点,且
两点,且 的周长为16,那么
的周长为16,那么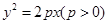 的焦点F的直线
的焦点F的直线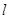 依次交抛物线及其准线于点A、B、C,若|BC |=2|BF|,且|AF|=3,则抛物线的方程是 。
依次交抛物线及其准线于点A、B、C,若|BC |=2|BF|,且|AF|=3,则抛物线的方程是 。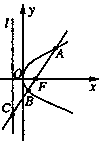
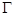 的长轴,点C在
的长轴,点C在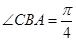 ,若AB=4,
,若AB=4,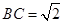 ,则
,则