题目内容
已知函数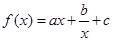 (
(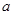 >0)的图象在点
>0)的图象在点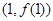 处的切线方程为
处的切线方程为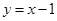 .
.
(1)用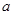 表示
表示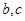 ;
;
(2)若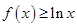 在
在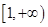 上恒成立,求
上恒成立,求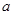 的取值范围;
的取值范围;
(3)证明:1+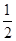 +
+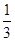 +…+
+…+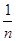 >
>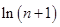 +
+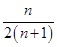
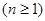 .
.
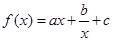 (
(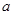 >0)的图象在点
>0)的图象在点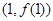 处的切线方程为
处的切线方程为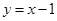 .
.(1)用
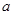 表示
表示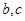 ;
;(2)若
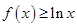 在
在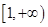 上恒成立,求
上恒成立,求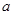 的取值范围;
的取值范围;(3)证明:1+
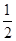 +
+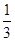 +…+
+…+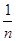 >
>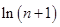 +
+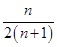
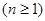 .
.(Ⅰ)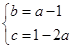 (II)
(II)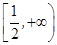 (Ⅲ)见解析
(Ⅲ)见解析
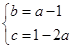 (II)
(II)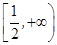 (Ⅲ)见解析
(Ⅲ)见解析(1)求函数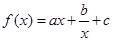 导数得
导数得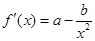 ,根据导数的几何意义得
,根据导数的几何意义得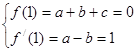 就可得到用
就可得到用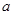 表示
表示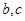 的式子;(2)若
的式子;(2)若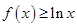 在
在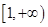 上恒成立,即
上恒成立,即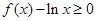 在
在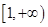 上恒成立。构造函数
上恒成立。构造函数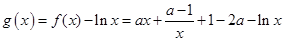 ,利用
,利用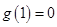 ,再讨论
,再讨论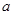 的取值范围研究
的取值范围研究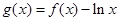 的单调性使
的单调性使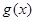 的最小值大于等于0可得
的最小值大于等于0可得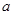 的取值范围;
的取值范围;
(3)由(2)知当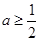 时,有
时,有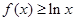 , (
, (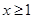 ) 若
) 若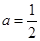 ,有
,有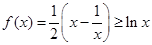 。结合要证的结论,令
。结合要证的结论,令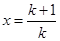 ,
,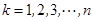 。分别把
。分别把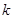 的值代入
的值代入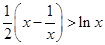 ,得到
,得到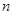 个不等式依次相加得
个不等式依次相加得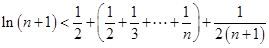 整理即得结论。本题是与自然数有关的问题也可用数学归纳法证明
整理即得结论。本题是与自然数有关的问题也可用数学归纳法证明
(Ⅰ)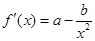 ,则有
,则有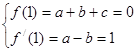 ,解得
,解得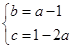 …3分
…3分
(II)由(Ⅰ)知,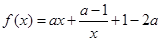
令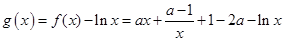 ,
,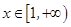
则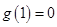 ,
,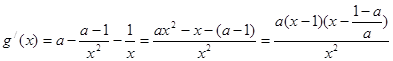 ……4分
……4分
(ⅰ)当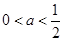 时,
时,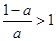 ,
,
若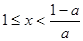 ,则
,则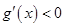 ,
,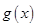 单调递减,所以
单调递减,所以 即
即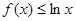 ,
,
故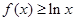 在
在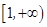 上不恒成立. …………6分
上不恒成立. …………6分
(ⅱ) 当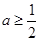 时,
时,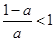 ,
,
若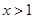 ,则
,则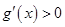 ,
,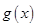 是增函数,所以
是增函数,所以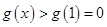
即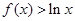 ,故当
,故当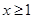 时,
时,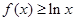 . …………8分
. …………8分
综上所述,所求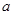 的取值范围为
的取值范围为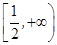 …………9分
…………9分
(Ⅲ)解法一:
由(Ⅱ)知,当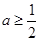 时,有
时,有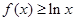 , (
, (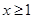 )
)
令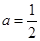 ,有
,有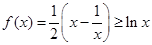 且当
且当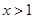 时,
时, 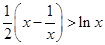 ……10分
……10分
令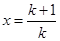 ,有
,有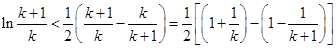
即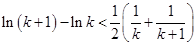 ,
, 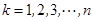 …………12分
…………12分
将上述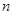 个不等式依次相加得
个不等式依次相加得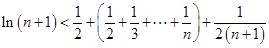
整理得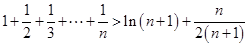 …………14分
…………14分
解法二: 用数学归纳法证明
(1) 当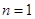 时,左边
时,左边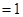 ,右边
,右边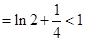 , 不等式成立.…………10分
, 不等式成立.…………10分
(2) 假设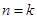 时, 不等式成立, 就是
时, 不等式成立, 就是
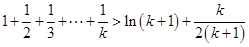
那么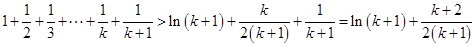
由(Ⅱ)知,当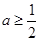 时,有
时,有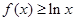 , (
, (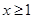 )
)
令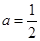 ,有
,有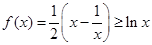 , (
, (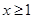 )
)
令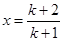 ,有
,有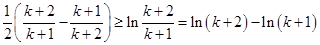
所以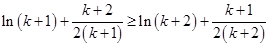
即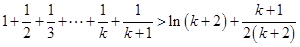
这就是说,当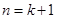 时, 不等式也成立。…………13分
时, 不等式也成立。…………13分
根据(1)和(2),可知不等式对任何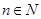 都成立。
都成立。
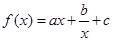 导数得
导数得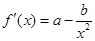 ,根据导数的几何意义得
,根据导数的几何意义得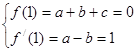 就可得到用
就可得到用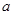 表示
表示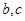 的式子;(2)若
的式子;(2)若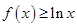 在
在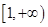 上恒成立,即
上恒成立,即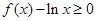 在
在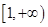 上恒成立。构造函数
上恒成立。构造函数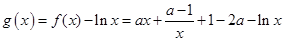 ,利用
,利用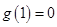 ,再讨论
,再讨论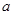 的取值范围研究
的取值范围研究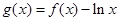 的单调性使
的单调性使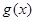 的最小值大于等于0可得
的最小值大于等于0可得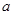 的取值范围;
的取值范围;(3)由(2)知当
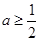 时,有
时,有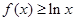 , (
, (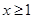 ) 若
) 若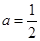 ,有
,有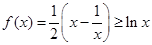 。结合要证的结论,令
。结合要证的结论,令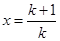 ,
,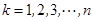 。分别把
。分别把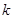 的值代入
的值代入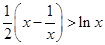 ,得到
,得到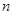 个不等式依次相加得
个不等式依次相加得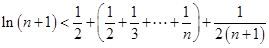 整理即得结论。本题是与自然数有关的问题也可用数学归纳法证明
整理即得结论。本题是与自然数有关的问题也可用数学归纳法证明(Ⅰ)
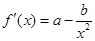 ,则有
,则有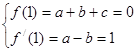 ,解得
,解得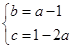 …3分
…3分(II)由(Ⅰ)知,
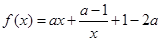
令
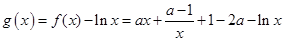 ,
,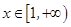
则
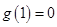 ,
,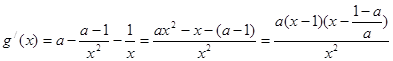 ……4分
……4分(ⅰ)当
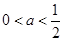 时,
时,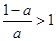 ,
,若
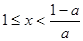 ,则
,则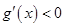 ,
,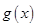 单调递减,所以
单调递减,所以 即
即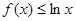 ,
,故
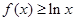 在
在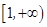 上不恒成立. …………6分
上不恒成立. …………6分(ⅱ) 当
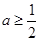 时,
时,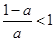 ,
,若
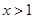 ,则
,则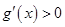 ,
,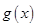 是增函数,所以
是增函数,所以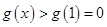
即
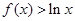 ,故当
,故当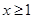 时,
时,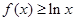 . …………8分
. …………8分综上所述,所求
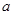 的取值范围为
的取值范围为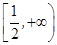 …………9分
…………9分(Ⅲ)解法一:
由(Ⅱ)知,当
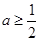 时,有
时,有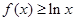 , (
, (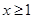 )
)令
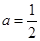 ,有
,有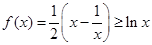 且当
且当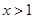 时,
时, 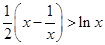 ……10分
……10分令
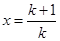 ,有
,有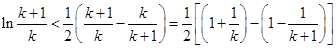
即
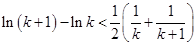 ,
, 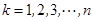 …………12分
…………12分将上述
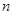 个不等式依次相加得
个不等式依次相加得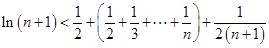
整理得
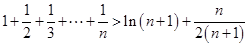 …………14分
…………14分解法二: 用数学归纳法证明
(1) 当
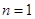 时,左边
时,左边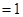 ,右边
,右边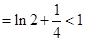 , 不等式成立.…………10分
, 不等式成立.…………10分(2) 假设
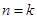 时, 不等式成立, 就是
时, 不等式成立, 就是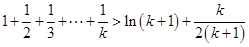
那么
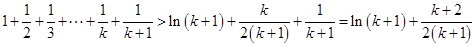
由(Ⅱ)知,当
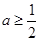 时,有
时,有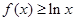 , (
, (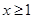 )
)令
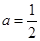 ,有
,有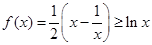 , (
, (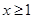 )
)令
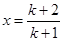 ,有
,有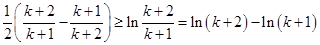
所以
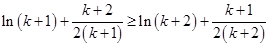
即
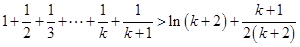
这就是说,当
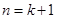 时, 不等式也成立。…………13分
时, 不等式也成立。…………13分根据(1)和(2),可知不等式对任何
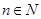 都成立。
都成立。
练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
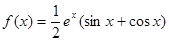 在区间
在区间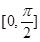 的值域为 ( )
的值域为 ( )



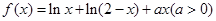 .
.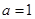 时,求
时,求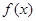 的单调区间;
的单调区间;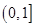 上的最大值为
上的最大值为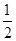 ,求
,求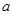 的值.
的值.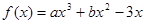 在
在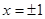 处取得极值,过点
处取得极值,过点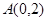 作曲线
作曲线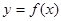 的切线
的切线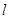 ,(1)求此切线
,(1)求此切线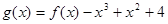 的图象围成的平面图形的面积。
的图象围成的平面图形的面积。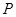 在曲线
在曲线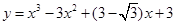 上移动,点
上移动,点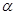 ,则角
,则角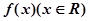 的导函数
的导函数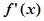 满足
满足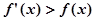 ,则当
,则当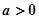 时,
时,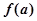 和
和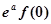 (
(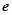 是自然对数的底数)大小关系为( ▲ )
是自然对数的底数)大小关系为( ▲ )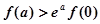
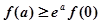
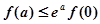

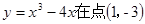 处的切线倾斜角为________.
处的切线倾斜角为________.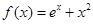 ,则
,则 .
.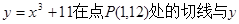 轴交点的纵坐标是( )
轴交点的纵坐标是( )