题目内容
设函数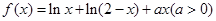 .
.
(Ⅰ) 当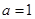 时,求
时,求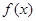 的单调区间;
的单调区间;
(Ⅱ) 若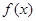 在
在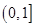 上的最大值为
上的最大值为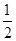 ,求
,求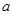 的值.
的值.
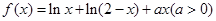 .
.(Ⅰ) 当
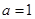 时,求
时,求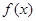 的单调区间;
的单调区间;(Ⅱ) 若
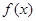 在
在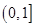 上的最大值为
上的最大值为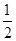 ,求
,求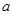 的值.
的值.(1)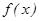 的单调递增区间为(0,
的单调递增区间为(0,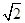 ),单调递减区间为(
),单调递减区间为(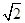 ,2);(2)a=1/2.
,2);(2)a=1/2.
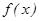 的单调递增区间为(0,
的单调递增区间为(0,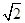 ),单调递减区间为(
),单调递减区间为(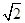 ,2);(2)a=1/2.
,2);(2)a=1/2.第一问中利用函数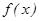 的定义域为(0,2),
的定义域为(0,2),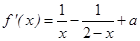 .
.
当a=1时,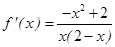 所以
所以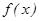 的单调递增区间为(0,
的单调递增区间为(0,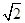 ),单调递减区间为(
),单调递减区间为(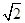 ,2);
,2);
第二问中,利用当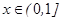 时,
时,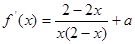 >0, 即
>0, 即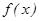 在
在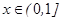 上单调递增,故
上单调递增,故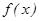 在
在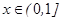 上的最大值为f(1)=a 因此a=1/2.
上的最大值为f(1)=a 因此a=1/2.
解:函数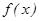 的定义域为(0,2),
的定义域为(0,2),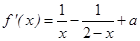 .
.
(1)当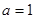 时,
时,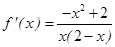 所以
所以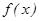 的单调递增区间为(0,
的单调递增区间为(0,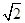 ),单调递减区间为(
),单调递减区间为(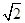 ,2);
,2);
(2)当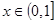 时,
时,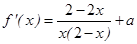 >0, 即
>0, 即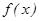 在
在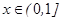 上单调递增,故
上单调递增,故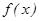 在
在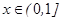 上的最大值为f(1)=a 因此a=1/2.
上的最大值为f(1)=a 因此a=1/2.
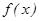 的定义域为(0,2),
的定义域为(0,2),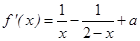 .
.当a=1时,
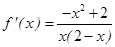 所以
所以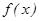 的单调递增区间为(0,
的单调递增区间为(0,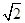 ),单调递减区间为(
),单调递减区间为(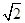 ,2);
,2);第二问中,利用当
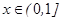 时,
时,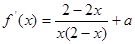 >0, 即
>0, 即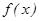 在
在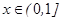 上单调递增,故
上单调递增,故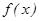 在
在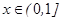 上的最大值为f(1)=a 因此a=1/2.
上的最大值为f(1)=a 因此a=1/2.解:函数
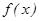 的定义域为(0,2),
的定义域为(0,2),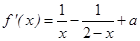 .
.(1)当
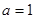 时,
时,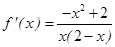 所以
所以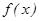 的单调递增区间为(0,
的单调递增区间为(0,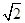 ),单调递减区间为(
),单调递减区间为(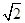 ,2);
,2);(2)当
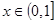 时,
时,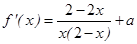 >0, 即
>0, 即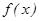 在
在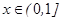 上单调递增,故
上单调递增,故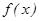 在
在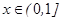 上的最大值为f(1)=a 因此a=1/2.
上的最大值为f(1)=a 因此a=1/2.
练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
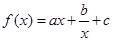 (
(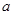 >0)的图象在点
>0)的图象在点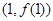 处的切线方程为
处的切线方程为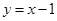 .
. ;
;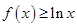 在
在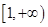 上恒成立,求
上恒成立,求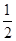 +
+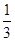 +…+
+…+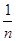 >
>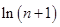 +
+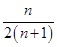
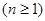 .
.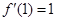 ,数列{
,数列{ }的前n项和
}的前n项和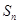 =f(n)(n∈N*).
=f(n)(n∈N*).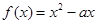
 }满足
}满足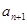 +
+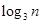 =
= 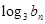 ,求数列{
,求数列{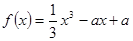
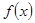 恰好有两个不同的零点,求
恰好有两个不同的零点,求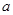 的值。
的值。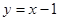 相切,求
相切,求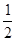 x
x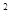 -ax+(a-1)
-ax+(a-1)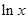 ,
,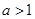 。讨论函数
。讨论函数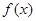 的单调性;
的单调性; 
 在
在 处的导数为-2,则
处的导数为-2,则
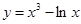 在点(1,2)处的切线方程为
在点(1,2)处的切线方程为 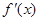 是
是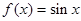 的导函数,则
的导函数,则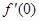 的值是 .
的值是 .